
【題目】如圖所示,折疊長方形(四個角都是直角)的一邊AD使點D落在BC邊的點F處,已知AB=DC=8cm,AD=BC=10cm,求EC的長.

【答案】EC的長為3cm.
【解析】
想求得EC長,利用勾股定理計算,需求得FC長,那么就需求出BF的長,利用勾股定理即可求得BF長.
設EC的長為xcm,則DE=(8﹣x)cm,
∵△ADE折疊后的圖形是△AFE,
∴AD=AF,∠D=∠AFE,DE=EF,
∵AD=BC=10cm,
∴AF=AD=10cm,
又∵AB=8cm,
在Rt△ABF中,根據勾股定理,得AB2+BF2=AF2,
∴82+BF2=102,
∴BF=6cm,
∴FC=BC﹣BF=10﹣6=4cm,
在Rt△EFC中,根據勾股定理,得:FC2+EC2=EF2,
∴42+x2=(8﹣x)2
即16+x2=64﹣16x+x2,
化簡,得16x=48,
∴x=3,
故EC的長為3cm.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,Rt△AOB的頂點O與原點重合,直角頂點A在x軸上,頂點B的坐標為(4,3),直線![]() 與x軸、y軸分別交于點D、E,交OB于點F.
與x軸、y軸分別交于點D、E,交OB于點F.
(1)寫出圖中的全等三角形及理由;
(2)求OF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人以相同路線前往距離單位10km的培訓中心參加學習.圖中l甲、l乙分別表示甲、乙兩人前往目的地所走的路程S(km)隨時間t(分)變化的函數圖象.以下說法:①乙比甲提前12分鐘到達;②甲的平均速度為15千米/小時;③乙走了8km后遇到甲;④乙出發6分鐘后追上甲.其中正確的有( ) 
A.4個
B.3個
C.2個
D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,二次函數y=﹣ ![]() x2+
x2+ ![]() x+2的圖象與x軸交于點A,B(點B在點A的左側),與y軸交于點C.過動點H(0,m)作平行于x軸的直線l,直線l與二次函數y=﹣
x+2的圖象與x軸交于點A,B(點B在點A的左側),與y軸交于點C.過動點H(0,m)作平行于x軸的直線l,直線l與二次函數y=﹣ ![]() x2+
x2+ ![]() x+2的圖象相交于點D,E.
x+2的圖象相交于點D,E.
(1)寫出點A,點B的坐標;
(2)若m>0,以DE為直徑作⊙Q,當⊙Q與x軸相切時,求m的值;
(3)直線l上是否存在一點F,使得△ACF是等腰直角三角形?若存在,求m的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學活動:探究利用角的對稱性構造全等三角形解決問題
(1)如圖①,OP是∠MON的平分線,請你利用該圖形畫一對以OP所在直線為對稱軸的全等三角形;(寫出簡單做法,不用證明兩三角形全等,不用尺規作圖亦可)
(2)如圖②,在△ABC中,∠ACB=90°,∠B=60°,AD、CE分別是∠BAC、∠BCA的平分線,AD、CE相交于點F.請直接填空:∠AFE= 度,DF EF(填>,<或=);
(3)如圖③,在△ABC中,如果∠ACB≠90°,而(2)中的其他條件不變,請問,你在(2)中所得結論是否仍然成立?若成立,請證明;若不成立,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
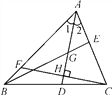
【題目】如圖所示,在△ABC中,∠1=∠2,G是AD的中點,延長BG交AC于點E,F為AB上一點,CF⊥AD交AD于點H.下列說法:①AD是△ABE的角平分線;②BE是△ABD的邊AD上的中線;③CH為△ACD的邊AD上的高;④AH是△ACF的角平分線和高線.其中正確的有_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正反比例函數的圖像交于![]() 、
、![]() 兩點,過第二象限的點
兩點,過第二象限的點![]() 作
作![]() 軸,點
軸,點![]() 的橫坐標為
的橫坐標為![]() ,且
,且![]() ,點
,點![]() 在第四象限
在第四象限
(1)求這兩個函數解析式;
(2)求這兩個函數圖像的交點坐標;
(3)若點![]() 在坐標軸上,聯結
在坐標軸上,聯結![]() 、
、![]() ,寫出當
,寫出當![]() 時的
時的![]() 點坐標
點坐標
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知![]() ,
,![]() 分別為兩坐標軸上的點,且
分別為兩坐標軸上的點,且![]() ,
,![]() 滿足
滿足![]() ,且
,且![]() .
.
(1)求![]() 、
、![]() 、
、![]() 三點的坐標;
三點的坐標;
(2)若![]() ,過點
,過點![]() 的直線分別交
的直線分別交![]() 、
、![]() 于
于![]() 、
、![]() 兩點,且
兩點,且![]() ,設
,設![]() 、
、![]() 兩點的橫坐標分別為
兩點的橫坐標分別為![]() 、
、![]() ,求
,求![]() 的值;
的值;
(3)如圖2,若![]() ,點
,點![]() 是
是![]() 軸上
軸上![]() 點右側一動點,
點右側一動點,![]() 于點
于點![]() ,在
,在![]() 上取點
上取點![]() ,使
,使![]() ,連接
,連接![]() ,當點
,當點![]() 在點
在點![]() 右側運動時,
右側運動時,![]() 的度數是否改變?若不變,請求其值;若改變,請說明理由.
的度數是否改變?若不變,請求其值;若改變,請說明理由.
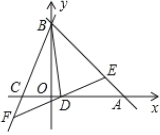
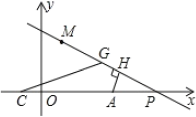
圖1 圖2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的大致圖象如圖所示(1<x=h<2,0<xA<1).下列結論:①2a+b>0;②abc<0; ③若OC=2OA,則2b﹣ac=4; ④3a﹣c<0.其中正確的個數是( ) 
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com