
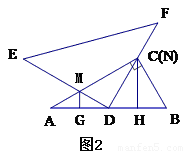
將一幅三角板Rt△ABC和Rt△DEF按如圖1擺放,點E, A, D, B在一條直線上,且D是AB的中點,將Rt△DEF繞點D順時針方向旋轉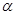 (0°<
(0°<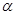 <90°)角,在旋轉過程中,直線DE與AC相交于點M,直線DF與BC相交于點N,分別過點M, N作直線AB的垂線,垂足分別為G, H.
<90°)角,在旋轉過程中,直線DE與AC相交于點M,直線DF與BC相交于點N,分別過點M, N作直線AB的垂線,垂足分別為G, H.
(1)當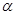 =30°時(如圖2),求證:AG=DH;
=30°時(如圖2),求證:AG=DH;
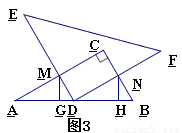
(2)當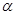 =60°時(如圖3),(1)中的結論是否仍成立?請寫出你的結論,并說明理由.
=60°時(如圖3),(1)中的結論是否仍成立?請寫出你的結論,并說明理由.
見解析.
【解析】
試題分析:(1)由α=30°知∠ADM=30°,∠A=30°,所以∠ADM=∠A.AM=DM.又由MG⊥AD于G,可得:AG= 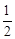 AD.又有∠CDB=180°-∠EDF-∠ADM=60°,∠B=60°,證得△CDB是等邊三角形.又CH⊥DB于H,DH=
AD.又有∠CDB=180°-∠EDF-∠ADM=60°,∠B=60°,證得△CDB是等邊三角形.又CH⊥DB于H,DH= 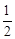 DB.根據直角三角形中30°所對直角邊是斜邊的一半得:BC=
DB.根據直角三角形中30°所對直角邊是斜邊的一半得:BC= 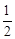 AB.由BC=BD,所以有AD=DB.從而證得AG=DH.
AB.由BC=BD,所以有AD=DB.從而證得AG=DH.
(2)在△AMD與△DNB中,∠A=∠NDB=30°,AD=DB,∠MDA=∠B=60°,可得△AMD≌△DNB,所以AM=DN.在△AMG與△DNH中,∠A=∠NDB,∠MGA=∠NHD=90°,又可證得△AMG≌△DNH.
∴AG=DH.
試題解析:(1)∵α=30°,∴∠ADM=30°,
∵∠A=30°,∴∠ADM=∠A.
∴AM=DM.
又∵MG⊥AD于G,
∴AG= 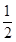 AD.
AD.
∵∠CDB=180°-∠EDF-∠ADM=60°,∠B=60°,
∴△CDB是等邊三角形.
又∵CH⊥DB于H,
∴DH= 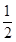 DB.
DB.
∵在△ABC中,∠ACB=90°,∠A=30°,
∴BC= 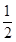 AB.
AB.
∵BC=BD,∴AD=DB.
∴AG=DH.
(2)結論成立.理由如下:
在△AMD與△DNB中,∠A=∠NDB=30°,AD=DB,∠MDA=∠B=60°,
∴△AMD≌△DNB,
∴AM=DN.
又∵在△AMG與△DNH中,∠A=∠NDB,∠MGA=∠NHD=90°,
∴△AMG≌△DNH.
∴AG=DH .
考點:1.等邊三角形的判定.2.直角三角形30°所對的直角邊等于斜邊的一半.3. 全等三角形判定和性質.


 同步輕松練習系列答案
同步輕松練習系列答案 課課通課程標準思維方法與能力訓練系列答案
課課通課程標準思維方法與能力訓練系列答案科目:初中數學 來源: 題型:閱讀理解

查看答案和解析>>
科目:初中數學 來源: 題型:
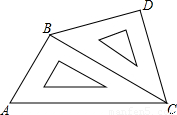
 小明將一幅三角板如圖所示擺放在一起,發現只要知道其中一邊的長就可以求出其它各邊的長.(兩個三角板分別是等腰直角三角形和含30°的直角三角形)
小明將一幅三角板如圖所示擺放在一起,發現只要知道其中一邊的長就可以求出其它各邊的長.(兩個三角板分別是等腰直角三角形和含30°的直角三角形)| 22+22 |
| 2 |
| 2 |
2
| ||
| 3 |
2
| ||
| 3 |
4
| ||
| 3 |
4
| ||
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
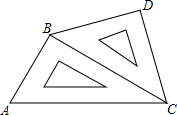 小明將一幅三角板如圖所示擺放在一起,發現只要知道其中一邊的長就可以求出其它各邊的長.(兩個三角板分別是等腰直角三角形和含30°的直角三角形)
小明將一幅三角板如圖所示擺放在一起,發現只要知道其中一邊的長就可以求出其它各邊的長.(兩個三角板分別是等腰直角三角形和含30°的直角三角形)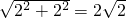
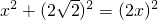
查看答案和解析>>
科目:初中數學 來源:2009-2010學年天津市河西區九年級(上)期末數學試卷(解析版) 題型:解答題
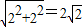
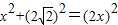
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com