
【題目】如圖,已知拋物線![]() 交
交![]() 軸于點
軸于點![]() 、點
、點![]() ,交
,交![]() 軸于點C,且S△ABC=6.
軸于點C,且S△ABC=6.
(1)求![]() 兩點的坐標;
兩點的坐標;
(2)求△ABC的外接圓與拋物線的對稱軸的交點坐標;
(3)點E為拋物線上的一動點(點![]() 異于
異于![]() ,且
,且![]() 在對稱軸右側),直線
在對稱軸右側),直線![]() 交對稱軸于N,
交對稱軸于N,
直線BE交對稱軸于![]() ,對稱軸交
,對稱軸交![]() 軸于
軸于![]() ,試確定
,試確定![]() 、
、![]() 的數量關系并說明理由.
的數量關系并說明理由.

【答案】(1)![]()
![]() ;(2)
;(2) 和
和 ;(3)
;(3)![]() 與
與![]() 的數量關系為
的數量關系為![]() (
(![]() 在
在![]() 軸下方)或
軸下方)或![]() (
(![]() 在
在![]() 軸上方)
軸上方)
【解析】試題分析:(1)設![]() ,
, ![]() ,根據題意和已知條件可得
,根據題意和已知條件可得![]() ,
, ![]() ,解得
,解得![]() ,
, ![]() ,即可得
,即可得![]() 兩點的坐標;(2))設
兩點的坐標;(2))設![]() 外接圓心為
外接圓心為![]() ,
, ![]() 交對稱軸于
交對稱軸于![]() ,設對稱軸交
,設對稱軸交![]() 軸于
軸于![]() ,作
,作![]() 對稱軸于
對稱軸于![]() ,可得
,可得![]() ,從而求得點D的坐標,根據勾股定理求得半徑的長,即可得△ABC的外接圓與拋物線的對稱軸的交點坐標;(3)分
,從而求得點D的坐標,根據勾股定理求得半徑的長,即可得△ABC的外接圓與拋物線的對稱軸的交點坐標;(3)分![]() 在
在![]() 軸下方和
軸下方和![]() 在
在![]() 軸上方兩種情況求
軸上方兩種情況求![]() 、
、![]() 的數量關系.
的數量關系.
試題解析:
(1)![]() ,
, ![]() ,
, ![]() ,
, ![]()
設![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]() ,
, ![]()
![]()
![]()
(2)設![]() 外接圓心為
外接圓心為![]() ,
, ![]() 交對稱軸于
交對稱軸于![]()
![]() ,
, ![]() 在直線
在直線![]() 上,設對稱軸交
上,設對稱軸交![]() 軸于
軸于![]() ,作
,作![]() 對稱軸于
對稱軸于![]()
![]()
![]() ,
, ![]() ,
, ![]()
 ,
,  ,
, 

(3)![]() ,
, ![]() ,
, ![]()
設![]() 的解析式為
的解析式為![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
設![]() 的解析式為
的解析式為![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()

![]() ,
, ![]()
![]() 即
即![]()
![]() 即
即![]()
①若![]() 在
在![]() 軸下方,則
軸下方,則![]() ,
, ![]()
![]()
②若![]() 在
在![]() 軸上方,則
軸上方,則![]() ,
, ![]()
![]()
![]() 與
與![]() 的數量關系為
的數量關系為![]() (
(![]() 在
在![]() 軸下方)或
軸下方)或![]() (
(![]() 在
在![]() 軸上方)
軸上方)


科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AD∥BC,∠ADC=90°,點E是BC邊上一動點,聯結AE,過點E作AE的垂線交直線CD于點F.已知AD=4cm,CD=2cm,BC=5cm,設BE的長為x cm,CF的長為y cm.

小東根據學習函數的經驗,對函數y隨自變量x的變化而變化的規律進行探究.下面是小東的探究過程,請補充完整:
(1)通過取點、畫圖、測量,得到了x與y的幾組值,如下表:

(說明:補全表格時相關數據保留一位小數)
(2)建立直角坐標系,描出以補全后的表中各對對應值為坐標的點,畫出該函數的圖象;

(3)結合畫出的函數圖象,解決問題: 當BE=CF時,BE的長度約為 cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若將一幅三角板按如圖所示的方式放置,則下列結論中不正確的是( )

A. ∠1=∠3 B. 如果∠2=30°,則有AC∥DE
C. 如果∠2=30°,則有BC∥AD D. 如果∠2=30°,必有∠4=∠C
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商品現在售價為每件60元,每星期可賣出300件,市場調查反映:調整價格,每件漲價1元,每星期要少賣出10件;每件降價1元,每星期可多賣出20件.已知商品的進價為每件40元.
(1)設每件降價x元,每星期的銷售利潤為y元;
① 請寫出y與x之間的函數關系式;
② 確定x的值,使利潤最大,并求出最大利潤;
(2)若漲價x元,則x= 元時,利潤y的最大值為 元(直接寫出答案,不必寫過程).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在長方形![]() 中,
中,![]() 。點
。點![]() 從
從![]() 出發,沿
出發,沿![]() 路線運動,到
路線運動,到![]() 停止;點
停止;點![]() 出發時的速度為每秒
出發時的速度為每秒![]() ,7秒時點
,7秒時點![]() 的速度變為每秒
的速度變為每秒![]() ,圖②是點
,圖②是點![]() 出發
出發![]() 秒后,
秒后,![]() 的面積
的面積![]() 與
與![]() (秒)的關系圖象;
(秒)的關系圖象;

(1)根據題目提供的信息,求出![]() 的值為______________、
的值為______________、![]() 的值為_________
的值為_________![]() 的值為___________;
的值為___________;
(2)設點![]() 離開點
離開點![]() 的路程為
的路程為![]() ,
,
①7.5秒時,![]() 的值為_____________________;
的值為_____________________;
②請求出當動點![]() 改變速度后,
改變速度后,![]() 與
與![]() 的關系式;
的關系式;
(3)點![]() 出發后幾秒,
出發后幾秒,![]() 的面積
的面積![]() 是長方形
是長方形![]() 面積的
面積的![]() ?并說明理由。
?并說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是平行四邊形,點E是邊CD上一點,且BC=EC,CF⊥BE交AB于點F,P是EB延長線上一點,下列結論:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正確結論的個數為( )
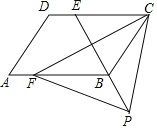
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,E是□ABCD的邊BC延長線上一點,AE交CD于點F,FG∥AD交AB于點G.
(1)填空:圖中與△CEF相似的三角形有__________;(寫出圖中與△CEF相似的所有三角形)
(2)從(1)中選出一個三角形,并證明它與△CEF相似.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某蔬菜有限公司一年四季都有大量新鮮蔬菜銷往全國各地,近年來它的蔬菜產值不斷增加,2014年蔬菜的產值是640萬元,2016年產值達到1000萬元.
(1)求2015年、2016年蔬菜產值的平均增長率是多少?
(2)若2017年蔬菜產值繼續穩定增長(即年增長率與前兩年的年增長率相同),那么請你估計2017年該公司的蔬菜產值達到多少萬元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com