
【題目】拋物線y=ax2+bx+c交x軸于A、B兩點,交y軸于點C,已知拋物線的對稱軸為x=1,B(3,0),C(0,﹣3),
(1)求二次函數y=ax2+bx+c的解析式;
(2)在拋物線對稱軸上是否存在一點P,使點P到B、C兩點距離之差最大?若存在,求出P點坐標;若不存在,請說明理由;
(3)平行于x軸的一條直線交拋物線于M、N兩點,若以MN為直徑的圓恰好與x軸相切,求此圓的半徑.
【答案】
(1)解:將C(0,﹣3)代入y=ax2+bx+c,
得c=﹣3.
將c=﹣3,B(3,0)代入y=ax2+bx+c,
得9a+3b+c=0.(1)
∵直線x=1是對稱軸,
∴ ![]() .(2)(2分)
.(2)(2分)
將(2)代入(1)得
a=1,b=﹣2.
所以,二次函數得解析式是y=x2﹣2x﹣3.
(2)解:AC與對稱軸的交點P即為到B、C的距離之差最大的點.
∵C點的坐標為(0,﹣3),A點的坐標為(﹣1,0),
∴直線AC的解析式是y=﹣3x﹣3,
又∵直線x=1是對稱軸,
∴點P的坐標(1,﹣6).
(3)解:設M(x1,y)、N(x2,y),所求圓的半徑為r, 
則x2﹣x1=2r,(1)
∵對稱軸為直線x=1,即 ![]() =1,
=1,
∴x2+x1=2.(2)
由(1)、(2)得:x2=r+1.(3)
將N(r+1,y)代入解析式y=x2﹣2x﹣3,
得y=(r+1)2﹣2(r+1)﹣3.
整理得:y=r2﹣4.
由所求圓與x軸相切,得到r=|y|,即r=±y,
當y>0時,r2﹣r﹣4=0,
解得, ![]() ,
, ![]() (舍去),
(舍去),
當y<0時,r2+r﹣4=0,
解得, ![]() ,
, ![]() (舍去).
(舍去).
所以圓的半徑是 ![]() 或
或 ![]() .
.
【解析】先利用待定系數法求出二次函數的解析式,然后再畫出函數圖象進行計算.


科目:初中數學 來源: 題型:
【題目】由線段a、b、c組成的三角形不是直角三角形的是( )
A.a=7,b=24,c=25
B.a= ![]() ,b=4,c=5
,b=4,c=5
C.a= ![]() ,b=1,c=
,b=1,c= ![]()
D.a= ![]() ,b=
,b= ![]() ,c=
,c= ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知:長江路西段與黃河路的夾角為150°,長江路東段與淮河路的夾角為135°,黃河路全長AC=20km,從A地道B地必須先走黃河路經C點后再走淮河路才能到達,城市道路改造后,直接打通長江路(即修建AB路段).問:打通長江路后從A地道B地可少走多少路程?(參考數據: ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中數學 來源: 題型:
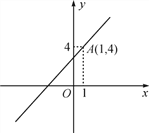
【題目】如圖,已知,一次函數y=kx+3的圖象經過點A(1,4).
(1)求這個一次函數的解析式;
(2)試判斷點B(-1,5),C(0,3),D(2,1)是否在這個一次函數的圖象上.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,∠BAC=90°,點D是BC上一點,將△ABD沿AD翻折后得到△AED,邊AE交BC于點F.


(1)如圖①,當AE⊥BC時,寫出圖中所有與∠B相等的角: ;所有與∠C相等的角: .
(2)若∠C-∠B=50°,∠BAD=x°(0<x≤45) .
① 求∠B的度數;
②是否存在這樣的x的值,使得△DEF中有兩個角相等.若存在,并求x的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“六一”前夕,某玩具經銷商用去2350元購進A,B,C三種新型的電動玩具共50套,并且購進的三種玩具都不少于10套,設購進A種玩具x套,B種玩具y套,三種電動玩具的進價和售價如表所示
型 號 | A | B | C |
進價(元/套) | 40 | 55 | 50 |
售價(元/套) | 50 | 80 | 65 |
(1)用含x、y的代數式表示購進C種玩具的套數;
(2)求y與x之間的函數關系式;
(3)假設所購進的這三種玩具能全部賣出,且在購銷這種玩具的過程中需要另外支出各種費用200元.
①求出利潤P(元)與x(套)之間的函數關系式;②求出利潤的最大值,并寫出此時三種玩具各多少套.
查看答案和解析>>
科目:初中數學 來源: 題型:
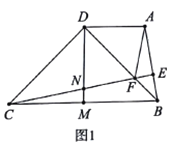
【題目】如圖1,四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 邊上的中線,過點
邊上的中線,過點![]() 作
作![]() 垂足為
垂足為![]() ,
,![]() 交線段
交線段![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() .
.
(1)求證:![]() ;
;
(2)探索線段![]() 和
和![]() 之間的數量關系,并證明你的結論;
之間的數量關系,并證明你的結論;
(3)當![]() 等于多少度時,點
等于多少度時,點![]() 恰好為
恰好為![]() 中點?
中點?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校準備購進一批節能燈,已知1只A型節能燈和3只B型節能燈共需26元;3只A型節能燈和2只B型節能燈共需29元.
(1)求一只A型節能燈和一只B型節能燈的售價各是多少元;
(2)學校準備購進這兩種型號的節能燈共50只,并且A型節能燈的數量不多于B型節能燈數量的3倍,請設計出最省錢的購買方案,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知矩形ABCD的三個頂點B(1,0),C(3,0),D(3,4).以A為頂點的拋物線y=ax2+bx+c過點C.動點P從點A出發,沿線段AB向點B運動.同時動點Q從點C出發,沿線段CD向點D運動.點P,Q的運動速度均為每秒1個單位.運動時間為t秒.過點P作PE⊥AB交AC于點E.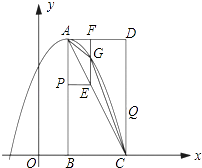
(1)直接寫出點A的坐標,并求出拋物線的解析式;
(2)過點E作EF⊥AD于F,交拋物線于點G,當t為何值時,△ACG的面積最大?最大值為多少?
(3)在動點P,Q運動的過程中,當t為何值時,在矩形ABCD內(包括邊界)存在點H,使以C,Q,E,H為頂點的四邊形為菱形?請直接寫出t的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com