科目：初中數學 來源： 題型：
問題提出
平面內不在同一條直線上的三點確定一個圓．那么平面內的四點(任意三點均不在同一
直線上），能否在同一個圓呢？
初步思考
設不在同一條直線上的三點A、B、C確定的圓為⊙O．
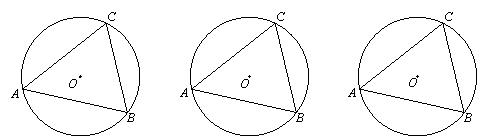
⑴當C、D在線段AB的同側時，
如圖①，若點D在⊙O上，此時有∠ACB＝∠ADB，理由是 ；
如圖②，若點D在⊙O內，此時有∠ACB ∠ADB；
如圖③，若點D在⊙O外，此時有∠ACB ∠ADB．（填“＝”、“＞”或“＜”）；
由上面的探究，請直接寫出A、B、C、D四點在同一個圓上的條件： ．
類比學習
（2）仿照上面的探究思路，請探究：當C、D在線段AB的異側時的情形．
 |
此時有 ， 此時有 ， 此時有 ．
由上面的探究，請用文字語言直接寫出A、B、C、D四點在同一個圓上的條件： ．
拓展延伸
（3）如何過圓上一點，僅用沒有刻度的直尺，作出已知直徑的垂線？
已知：如圖，AB是⊙O的直徑，點C在⊙O上．
求作：CN⊥AB．
作法：①連接CA，
CB；
②在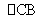
上任取異于B、C的一點D，連接DA，DB；
③DA與CB相交于E點，延長AC、BD，交于F點；
④連接F、E并延長，交直徑AB于M；
⑤連接D、M并延長，交⊙O于N．連接CN．
則CN⊥AB．
請按上述作法在圖④中作圖，并說明CN⊥AB的理由．（提示：可以利用（2）中的結論）
查看答案和解析>>
科目：初中數學 來源： 題型：
投擲一枚質地均勻的正方體骰子.
（1）下列說法中正確的有 ．（填序號）
①向上一面點數為1點和3點的可能性一樣大；
②投擲6次，向上一面點數為1點的一定會出現1次；
③連續投擲2次，向上一面的點數之和不可能等于13．
（2）如果小明連續投擲了10次，其中有3次出現向上一面點數為6點，這時小明說：投擲正方體骰子，向上一面點數為6點的概率是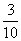
．你同意他的說法嗎？說說你的理由．
（3）為了估計投擲正方體骰子出現6點朝上的
概率，小亮采用轉盤來代替骰子做實驗．下圖是一個可以自由轉動的轉盤，請你將轉盤分為2個扇形區域，分別涂上紅、白兩種顏色，使得轉動轉盤，當轉盤停止轉動后，指針落在紅色區域的概率與投擲正方體骰子出現6點朝上的概率相同．
|
查看答案和解析>>
科目：初中數學 來源： 題型：
下列命題正確的是（ ）
A、垂直于半徑的直線一定是圓的切線
B、正三角形繞其中心旋轉180°后能與原圖形重合是必然事件
C、有一組對邊平行，一組對角相等的四邊形是平行四邊形
D
、四個角都是直角的四邊形是正方形
查看答案和解析>>
科目：初中數學 來源： 題型：
書籍是人類進步的階梯.聯合國教科文組織把每年的4月23日確定為“世界讀書日”．某校為了了解該校學生一個學期閱讀課外書籍的情況，在全校范圍內隨機對100名學生進行了問卷調查，根據調查的結果，繪制了統計圖表的一部分：
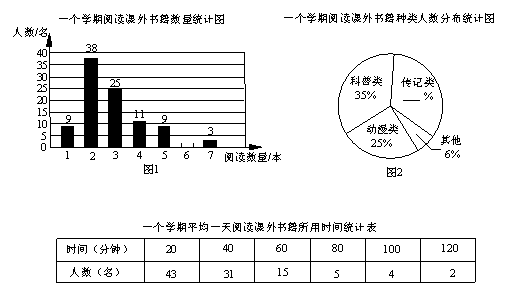
請你根據以上信息解答下列問題：
（1）補全圖1、圖2；
（2）這100名學生一個學期平均每人閱讀課外書籍多少本？若該校共有4000名學生，請你估計這個學校學生一個學期閱讀課外書籍共多少本？
（3）根據統計表，求一個學期平均一天閱讀課外書籍所用時間的眾數和中位數.
查看答案和解析>>
科目：初中數學 來源： 題型：
等腰三角形的一個內角為50°，則另外兩個角的度數分別為（ ）
A． 65°,65° B． 50°,80°
C．65°,65°或50°,80° D． 50°,50°
查看答案和解析>>
科目：初中數學 來源： 題型：
一個一次函數圖象與直線y=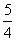
x+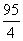
平行，與x軸、y軸的交點分別為A、B，并且過點（-1，-20），則在線段AB上（包括端點A、B），橫、縱坐標都是整數的點有 個．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的最簡公分母是 .
，則在旋轉過程中點D到D’的路徑長是＿＿＿＿