
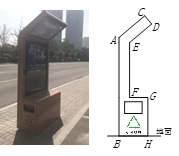
【題目】在太原迎澤西大街上有一種智能垃圾桶,這種智能垃圾桶不僅可以供行人休息,燈箱邊的中部還有USB接口可供行人充電.此種垃圾桶的側面示意圖如圖所示,其中AC∥ED,AB∥EF∥GH,CD=20cm,DE=60cm,EF=100m,GH=80cm,∠CDE=∠EFG=90°,∠DEF=130°,則此種垃圾桶的高度(C到地面的距離)約為________cm.(參考數據:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
【答案】233.8
【解析】
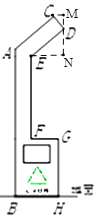
如圖,過點E作EN⊥EF,過點D作MN⊥EN于N,過點C作CM⊥MN于M,可得∠DEN=40°,根據角的和差關系可得∠CDM=∠DEN=40°,利用∠CDM和∠DEN的三角函數可求出MD和DN的長,根據垃圾桶的高度為MD+DN+EF+GH即可得答案.
如圖,過點E作EN⊥EF,過點D作MN⊥EN于N,過點C作CM⊥MN于M,
∴∠END=90°,∠M=90°,
∵∠DEF=130°,
∴∠DEN=∠DEF-90°=40°,
∵∠CDE=90°,
∴∠DEN+∠EDN=90°,∠CDM+∠EDN=90°,
∴∠CDM=∠DEN=40°,
∵CD=20cm,DE=60cm,
∴DM=CD·cos∠CDM≈20×0.77=15.4cm,DN=DE·sin∠DEN≈60×0.64=38.4cm,
∴DM+DN+EF+GH=15.4+38.4+80+100=233.8cm,
∴此種垃圾桶的高度約為233.8cm.
故答案為:233.8


科目:初中數學 來源: 題型:
【題目】某跳高集訓隊,對集訓隊員進行了一次跳高測試,經過統(tǒng)計,將集訓隊員的測試成績(單位:m),繪制成尚不完整的扇形統(tǒng)計圖(圖①)與條形統(tǒng)計圖(圖②).
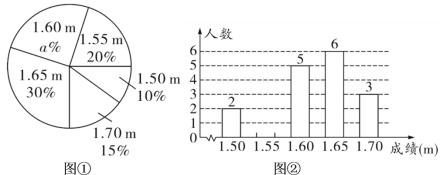
(1)![]() ________,請將條形統(tǒng)計圖補充完整;
________,請將條形統(tǒng)計圖補充完整;
(2)求集訓隊員測試成績的眾數;
(3)教練發(fā)現,測試成績不包括兩名請假的隊員,補測后,把這兩名隊員的成績(均是0.05的整數倍)與原測試成績并成一組新數據,求新數據的中位數.
查看答案和解析>>
科目:初中數學 來源: 題型:
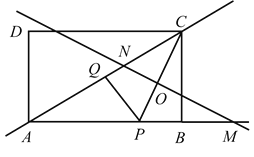
【題目】如圖,矩形![]() 中,AB=8,BC=6,點
中,AB=8,BC=6,點![]() 是射線
是射線![]() 上一動點,設
上一動點,設![]() .過點
.過點![]() 做射線
做射線![]() 的垂線段
的垂線段![]() ,垂足為
,垂足為![]() ,作
,作![]() 的垂直平分線
的垂直平分線![]() 交射線
交射線![]() 于點
于點![]() ,交直線
,交直線![]() 于
于![]() .
.
![]() 點
點![]() 在邊
在邊![]() 上時.①用含
上時.①用含![]() 的代數式表示
的代數式表示![]() .②當
.②當![]() 時,直線ON交射線CD于
時,直線ON交射線CD于![]() ,求CE的長.
,求CE的長.
![]() 當
當![]() 為何值時,過
為何值時,過![]() 三點的圓與矩形
三點的圓與矩形![]() 的邊或對角線
的邊或對角線![]() 相切.
相切.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了鍛煉學生身體素質,訓練定向越野技能,某校在一公園內舉行定向越野挑戰(zhàn)賽.路線圖如圖![]() 所示,點
所示,點![]() 為矩形
為矩形![]() 邊
邊![]() 的中點,在矩形
的中點,在矩形![]() 的四個頂點處都有定位儀,可監(jiān)測運動員的越野進程,其中一位運動員
的四個頂點處都有定位儀,可監(jiān)測運動員的越野進程,其中一位運動員![]() 從點
從點![]() 出發(fā),沿著
出發(fā),沿著![]() 的路線勻速行進,到達點
的路線勻速行進,到達點![]() .設運動員
.設運動員![]() 的運動時間為
的運動時間為![]() ,到監(jiān)測點的距離為
,到監(jiān)測點的距離為![]() .現有
.現有![]() 與
與![]() 的函數關系的圖象大致如圖
的函數關系的圖象大致如圖![]() 所示,則這一信息的來源是( ).
所示,則這一信息的來源是( ).


A. 監(jiān)測點![]() B. 監(jiān)測點
B. 監(jiān)測點![]() C. 監(jiān)測點
C. 監(jiān)測點![]() D. 監(jiān)測點
D. 監(jiān)測點![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在△ABC中,∠ACB=90°,AC=BC,E為∠ACB平分線CD上一動點(不與點C重合),點E關于直線BC的對稱點為F,連接AE并延長交CB延長線于點H,連接FB并延長交直線AH于點G.
(1)求證:AE=BF.
(2)用等式表示線段FG,EG與CE的數量關系,并證明.
(3)連接GC,用等式表示線段GE,GC與GF的數量關系是 .
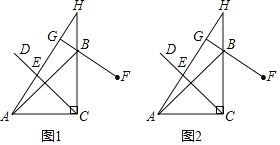
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與實踐
問題情境
數學活動課上,老師讓同學們根據如下問題情境,發(fā)現并提出問題.
如圖1,△ABC與△EDC都是等腰直角三角形,點E,D分別在AC和BC上,連接EB.將線段EB繞點B順時針旋轉90°,得到的對應線段為BF.連接DF.“興趣小組”提出了如下兩個問題:①AE=BD,AE⊥BD;②DF=AB,DF⊥AB.
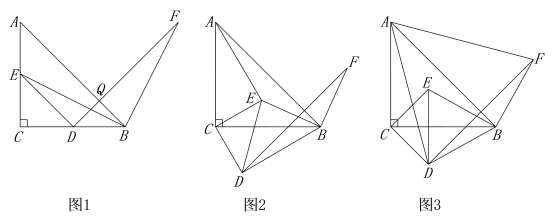
解決問題:
(1)請你證明“興趣小組”提出的第②個問題.
探索發(fā)現:
(2)“實踐小組”在圖1的基礎上,將△EDC繞點C順時針旋轉角度![]() (0°<
(0°<![]() <90°),其它條件保持不變,得到圖2.
<90°),其它條件保持不變,得到圖2.
①請你幫助“實踐小組”探索:“興趣小組”提出的兩個問題是否還成立?如果成立,請給出證明;若不成立,請說明理由.
②如圖3,當AD=AF時,請求出此時旋轉角α的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在北京市開展的“首都少年先鋒崗”活動中,某數學小組到人民英雄紀念碑站崗執(zhí)勤,并在活動后實地測量了紀念碑的高度. 方法如下:如圖,首先在測量點A處用高為1.5m的測角儀AC測得人民英雄紀念碑MN頂部M的仰角為35°,然后在測量點B處用同樣的測角儀BD測得人民英雄紀念碑MN頂部M的仰角為45°,最后測量出A,B兩點間的距離為15m,并且N,B,A三點在一條直線上,連接CD并延長交MN于點E. 請你利用他們的測量結果,計算人民英雄紀念碑MN的高度.
(參考數據:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)

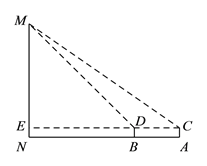
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O中,FG、AC是直徑,AB是弦,FG⊥AB,垂足為點P,過點C的直線交AB的延長線于點D,交GF的延長線于點E,已知AB=4,⊙O的半徑為![]() .
.
(1)分別求出線段AP、CB的長;
(2)如果OE=5,求證:DE是⊙O的切線;
(3)如果tan∠E=![]() ,求DE的長.
,求DE的長.
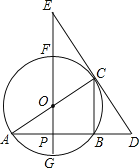
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com