
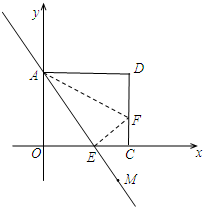 如圖,把矩形紙片AOCD置于直角坐標系中,O為坐標原點,
如圖,把矩形紙片AOCD置于直角坐標系中,O為坐標原點,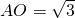 ,把矩形紙片沿直線AF折疊,使得點D與OC上的點E重合,這時AE平分∠OAF.
,把矩形紙片沿直線AF折疊,使得點D與OC上的點E重合,這時AE平分∠OAF. ,
, )、E(1,0),
)、E(1,0),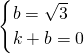 ,解得:
,解得: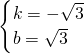
 x+
x+ ;
; -y,
-y, -y,解得
-y,解得 ,
, CF=1,
CF=1, );
);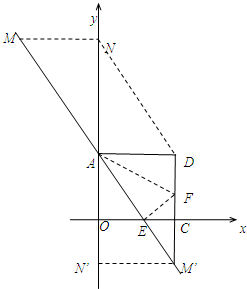 存在.理由如下:
存在.理由如下: AD=2
AD=2 ,
,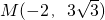 ;
;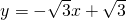 上,當x=2時,
上,當x=2時,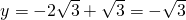 ,
,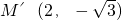
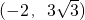 或
或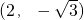 .
. )、E(1,0),再利用待定系數法即可求出直線AE的解析式;設點F的坐標(x,y),利用折疊的性質和含30°的直角三角形三邊的關系可得到CF=
)、E(1,0),再利用待定系數法即可求出直線AE的解析式;設點F的坐標(x,y),利用折疊的性質和含30°的直角三角形三邊的關系可得到CF= ,EC=1,即可得到F點的坐標.
,EC=1,即可得到F點的坐標. AD=2
AD=2 ,即可得到M點的坐標;同理可得當延長DC交直線AE于點M',則DM'∥AO,作M'N'⊥y軸于點N',則M'N'∥AD,求出點M′的坐標.
,即可得到M點的坐標;同理可得當延長DC交直線AE于點M',則DM'∥AO,作M'N'⊥y軸于點N',則M'N'∥AD,求出點M′的坐標.

科目:初中數學 來源: 題型:
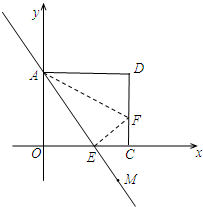 如圖,把矩形紙片AOCD置于直角坐標系中,O為坐標原點,AO=
如圖,把矩形紙片AOCD置于直角坐標系中,O為坐標原點,AO=| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com