
| 1 |
| 2 |
| 1 |
| 2 |


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
 △ACB紙片的斜邊AC上,直角邊DF落在AC所在的直線上。
△ACB紙片的斜邊AC上,直角邊DF落在AC所在的直線上。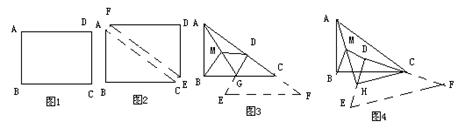
查看答案和解析>>
科目:初中數學 來源:2011-2012學年浙江省杭州市余杭區星橋中學八年級第一學期期中考試數學卷 題型:解答題
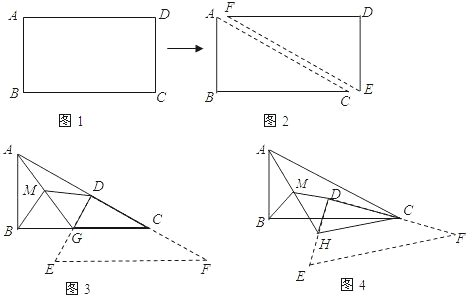
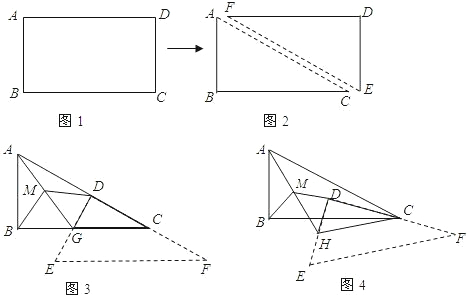
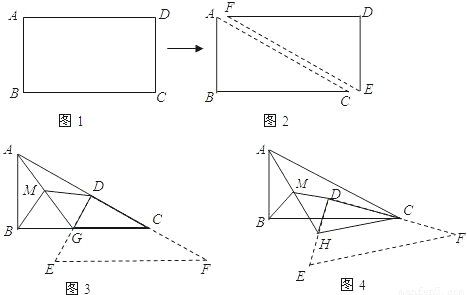
小華將一張矩形紙片(如圖1)沿對角線AC剪開,得到兩張三角形紙片(如圖2),其中∠ACB=β,然后將這兩張三角形紙片按如圖3所示的位置擺放,△EFD紙片的直角頂點D落在 △ACB紙片的斜邊AC上,直角邊DF落在AC所在的直線上。
△ACB紙片的斜邊AC上,直角邊DF落在AC所在的直線上。
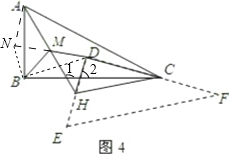
【小題1】(1)若DE與BC相交于點G,取AG的中點M,連結MB,MD,當△EFD紙片沿CA方向平移時(如圖3),請你猜想并寫出MB與MD的數量關系,然后證明你的猜想;(3分)
【小題2】(2)在(1)的條件下,求出∠BMD的大小(用含β的式子表示),并說明當β=45o時,△BMD是什么三角形;(5分)
【小題3】(3)在圖3的基礎上,將△EFD紙片繞點C逆時針旋轉一定的角度(小于90o),此時△CGD變成△CHD,同樣取AH的中點M,連結MB,MD(如圖4),請繼續探究MB與MD的數量關系和∠BMD的大小,直接寫出你的猜想,不證明,并說明β為何值時△BMD為等邊三角形。(2分)
查看答案和解析>>
科目:初中數學 來源:2011-2012年浙江省杭州市八年級第一學期期中考試數學卷 題型:解答題
小華將一張矩形紙片(如圖1)沿對角線AC剪開,得到兩張三角形紙片(如圖2),其中∠ACB=β,然后將這兩張三角形紙片按如圖3所示的位置擺放,△EFD紙片的直角頂點D落在△ACB紙片的斜邊AC上,直角邊DF落在AC所在的直線上。

1.(1)若DE與BC相交于點G,取AG的中點M,連結MB,MD,當△EFD紙片沿CA方向平移時(如圖3),請你猜想并寫出MB與MD的數量關系,然后證明你的猜想;(3分)
2.(2)在(1)的條件下,求出∠BMD的大小(用含β的式子表示),并說明當β=45o時,△BMD是什么三角形;(5分)
3.(3)在圖3的基礎上,將△EFD紙片繞點C逆時針旋轉一定的角度(小于90o),此時△CGD變成△CHD,同樣取AH的中點M,連結MB,MD(如圖4),請繼續探究MB與MD的數量關系和∠BMD的大小,直接寫出你的猜想,不證明,并說明β為何值時△BMD為等邊三角形。(2分)
查看答案和解析>>
科目:初中數學 來源:2010年河北省張家口市橋東區中考數學一模試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com