
【題目】工廠準(zhǔn)備購進(jìn)一批節(jié)能燈,已知1只A型節(jié)能燈和3只B型節(jié)能燈共需26元;3只A型節(jié)能燈和2只B型節(jié)能燈共需29元.
(1)求一只A型節(jié)能燈和一只B型節(jié)能燈的售價各是多少元;
(2)工廠準(zhǔn)備購進(jìn)這兩種型號的節(jié)能燈共50只,且A型節(jié)能燈的數(shù)量不多于B型節(jié)能燈數(shù)量的4倍,如何購買A、B型節(jié)能燈,可以使總費(fèi)用最少,且總費(fèi)用最少是多少.
【答案】(1)A型5元,B型7元;(2)A型40只,B型10只,總費(fèi)用270元.
【解析】
(1)設(shè)一只A型節(jié)能燈的售價是x元,一只B型節(jié)能燈的售價是y元,根據(jù):“1只A型節(jié)能燈和3只B型節(jié)能燈共需26元;3只A型節(jié)能燈和2只B型節(jié)能燈共需29元”列方程組求解即可;
(2)首先根據(jù)“A型節(jié)能燈的數(shù)量不多于B型節(jié)能燈數(shù)量的4倍”確定自變量的取值范圍,然后得到有關(guān)總費(fèi)用和A型燈的只數(shù)之間的關(guān)系得到函數(shù)解析式,確定函數(shù)的最值即可.
解:(1)設(shè)一只A型節(jié)能燈的售價是x元,一只B型節(jié)能燈的售價是y元,
根據(jù)題意,得:![]() ,解得:
,解得:![]() ,
,
(2)設(shè)購進(jìn)A型節(jié)能燈a只,則購進(jìn)B型節(jié)能燈(50-a)只,
總費(fèi)用為:![]() ,
,
∵且A型節(jié)能燈的數(shù)量不多于B型節(jié)能燈數(shù)量的4倍,即![]() ,
,
解得:![]() ,
,
而a為正整數(shù),
∴當(dāng)a=40時,總費(fèi)用最少,總費(fèi)用為:-80+350=270元,
∴購進(jìn)B型節(jié)能燈(50-a)=50-40=10只.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 是☉
是☉![]() 的直徑,
的直徑,![]() 為☉
為☉![]() 上一點(diǎn),
上一點(diǎn),![]() 是半徑
是半徑![]() 上一動點(diǎn)(不與
上一動點(diǎn)(不與![]() 重合),過點(diǎn)
重合),過點(diǎn)![]() 作射線
作射線![]() ,分別交弦
,分別交弦![]() ,
,![]() 于
于![]() 兩點(diǎn),過點(diǎn)
兩點(diǎn),過點(diǎn)![]() 的切線交射線
的切線交射線![]() 于點(diǎn)
于點(diǎn)![]() .
.
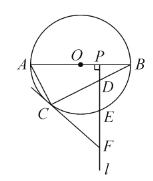
(1)求證:![]() .
.
(2)當(dāng)![]() 是
是![]() 的中點(diǎn)時,
的中點(diǎn)時,
①若![]() ,判斷以
,判斷以![]() 為頂點(diǎn)的四邊形是什么特殊四邊形,并說明理由;
為頂點(diǎn)的四邊形是什么特殊四邊形,并說明理由;
②若![]() ,且
,且![]() ,則
,則![]() _________.
_________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
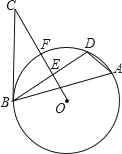
【題目】如圖,△ABD是⊙O的內(nèi)接三角形,E是弦BD的中點(diǎn),點(diǎn)C是⊙O外一點(diǎn)且∠DBC=∠A,連接OE延長與圓相交于點(diǎn)F,與BC相交于點(diǎn)C.
(1)求證:BC是⊙O的切線;
(2)若⊙O的半徑為6,BC=8,求弦BD的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,![]() 中,
中,![]() 是
是![]() 邊上一點(diǎn),
邊上一點(diǎn),![]() 是
是![]() 的中點(diǎn),過點(diǎn)
的中點(diǎn),過點(diǎn)![]() 作
作![]() 的平行線交
的平行線交![]() 的延長線于
的延長線于![]() ,且
,且![]() ,連接
,連接![]() .
.
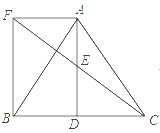
(1)求證:![]() 是
是![]() 的中點(diǎn);
的中點(diǎn);
(2)若![]() ,試判斷四邊形
,試判斷四邊形![]() 的形狀,并證明你的結(jié)論.
的形狀,并證明你的結(jié)論.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,二次函數(shù)y=ax2+bx+c的圖象所示,下列結(jié)論中:①abc>0;②2a+b=0;③當(dāng)m≠1時,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,則x1+x2=2,其中正確的結(jié)論分別是___.
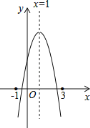
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
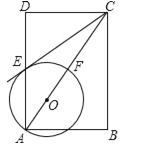
【題目】如圖,在矩形ABCD中,點(diǎn)O在對角線AC上,以OA的長為半徑的圓O與AD、AC分別交于點(diǎn)E、F,且∠ACB=∠DCE.
(1)判斷直線CE與⊙O的位置關(guān)系,并證明你的結(jié)論;
(2)若tan∠ACB=![]() ,BC=2,求⊙O的半徑.
,BC=2,求⊙O的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
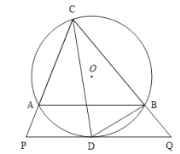
【題目】如圖,![]() 內(nèi)接于
內(nèi)接于![]() ,
,![]() 平分
平分![]() 交
交![]() 于
于![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 的切線
的切線![]() 分別交
分別交![]() 、
、![]() 的延長線于
的延長線于![]() 、
、![]() ,連接
,連接![]() .
.
(1)求證:![]() ;
;
(2)連![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,且
,且![]() ,求弦
,求弦![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
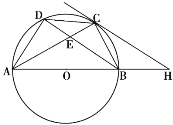
【題目】如圖,點(diǎn)A,B,C,D是直徑為AB的⊙O上四個點(diǎn),C是劣弧![]() 的中點(diǎn),AC交BD于點(diǎn)E,AE=2,EC=1.
的中點(diǎn),AC交BD于點(diǎn)E,AE=2,EC=1.
(1)求證:△DEC∽△ADC;
(2)連結(jié)DO,探究四邊形OBCD是否是菱形?若是,請你給予證明;若不是,請說明理由;
(3)延長AB到H,使BH=OB,求證:CH是⊙O的切線.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】一輛貨車早晨7∶00出發(fā),從甲地駛往乙地送貨.如圖是貨車行駛路程y(km)與行駛時間x(h)的完整的函數(shù)圖像(其中點(diǎn)B、C、D在同一條直線上),小明研究圖像得到了以下結(jié)論:
①甲乙兩地之間的路程是100 km;
②前半個小時,貨車的平均速度是40 km/h;
③8∶00時,貨車已行駛的路程是60 km;
④最后40 km貨車行駛的平均速度是100 km/h;
⑤貨車到達(dá)乙地的時間是8∶24,
其中,正確的結(jié)論是( )

A.①②③④B.①③⑤C.①③④D.①③④⑤
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com