【題目】如圖，在平面直角坐標系
中，正方形ABCO的對角線BO在x 軸上，若正方形ABCO的邊長為
，點B在x負半軸上，反比例函數
的圖象經過C點．
（1）求該反比例函數的解析式；
（2）當函數值
＞-2時，請直接寫出自變量x的取值范圍；
（3）若點P是反比例函數上的一點，且△PBO的面積恰好等于正方形ABCO的面積，求點P的坐標．
優翼小幫手同步口算系列答案科目：初中數學 來源： 題型：
【題目】已知，如圖，在平面直角坐標系中，點A坐標為（﹣2，0），點B坐標為（0，2），點E為線段AB上的動點（點E不與點A，B重合），以E為頂點作∠OET=45°，射線ET交線段0B于點F，C為y軸正半軸上一點，且OC=AB，拋物線y=﹣ 
x2+mx+n的圖象經過A，C兩點． 
（1）求此拋物線的函數表達式；
（2）求證：∠BEF=∠AOE；
（3）當△EOF為等腰三角形時，求此時點E的坐標；
（4）在（3）的條件下，當直線EF交x軸于點D，P為（1）中拋物線上一動點，直線PE交x軸于點G，在直線EF上方的拋物線上是否存在一點P，使得△EPF的面積是△EDG面積的（2 +1）倍？若存在，請直接寫出點P的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，正方形ABCD中，點E、F分別在邊DC、AD上，且AE⊥BF于G． 
（1）求證：BF=AE；
（2）如圖2，當點E在DC延長線上，點F在AD延長線上時，（1）中結論是否成立？（直接寫結論） 
（3）在圖2中，若點M、N、P、Q分別為四邊形AFEB四條邊AF、EF、EB、AB的中點，且AF：AD=4：3，求S四邊形MNPQ：S正方形ABCD ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，有甲、乙兩個可以自由轉動的轉盤，其中轉盤甲被平均分成三個扇形，轉盤乙被平均分成五個扇形，小明與小亮玩轉盤游戲，規則如下：同時轉動兩個轉盤，轉盤停止后，轉盤中甲指針所指數字作為點的橫坐標，轉盤乙指針所指數字作為點的縱坐標，從而確定一個點的坐標為A（m，n）．當點A在第一象限時，小明贏；當點A在第二象限時，小亮贏．請你利用畫樹狀圖或列表法分析該游戲規則對雙方是否公平？并說明理由．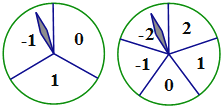
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知，在△ABC中，∠BAC=90°，∠ABC=45°，點D為直線BC上一動點（點D不與點B，C重合）．以AD為邊作正方形ADEF，連接CF.
（1）如圖1，當點D在線段BC上時．求證：CF+CD=BC；
（2）如圖2，當點D在線段BC的延長線上時，其他條件不變，請直接寫出CF，BC，CD三條線段之間的關系；
（3）如圖3，當點D在線段BC的反向延長線上時，且點A，F分別在直線BC的兩側，其他條件不變；
①請直接寫出CF，BC，CD三條線段之間的關系；
②若正方形ADEF的邊長為2
，對角線AE，DF相交于點O，連接OC．求OC的長度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，O是矩形ABCD的對角線的交點，作DE∥AC，CE∥BD，DE、CE相交于點E．求證：
（1）四邊形OCED是菱形．
（2）連接OE，若AD=4，CD=3，求菱形OCED的周長和面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
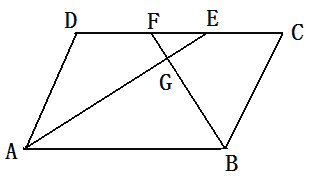
【題目】平行四邊形ABCD中， AE、BF分別平分∠DAB和∠ABC交CD于點E、F.AE、BF交于點G.
(1)求證AE⊥BF
(2)判斷DE和CF的大小關系，并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某經銷商銷售一種圓盤，圓盤的半徑x（cm），圓盤的售價y與x成正比例，圓盤的進價與x2成正比例，售出一個圓盤的利潤是P（元）．當x=10時，y=80，p=30．（利潤=售價﹣進價）．
（1）求y與x滿足的函數關系式；
（2）求P與x滿足的函數關系式；
（3）當售出一個圓盤所獲得的利潤是32元時，求這個圓盤的半徑．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
