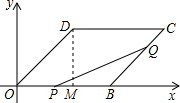
解:(1)過點D作DM⊥OB于M,
∵平行四邊形OBCD中,OB=8cm,BC=6cm,∠DOB=45°,
∴OD=BC=6cm,
∴OM=DM=OD•sin45°=6×

=3

,
∴D(3

,3

),B(8,0),
設經過O,B,D三點的拋物線的解析式為:y=ax(x-8),
將D的坐標代入得:3

=3

a•(3

-8),
解得:a=-
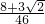
,
∴y=-
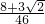
x(x-8);
(2)∵∠PBQ=180°-∠DOB=135°,
∴若△PBQ為等腰三角形,則PB=BQ.
設P,Q移動t秒時,△PBQ為等腰三角形,
∴P點走過的路程為t,Q點走過的路程為t,
∴PB=OB-t=8-t(cm),BQ=tcm.
若PB=BQ,
則8-t=t,
解得:t=4(s).
∴P,Q移動4秒時,△PBQ為等腰三角形;
(3)如圖:過點D作DM⊥OB于M,過點P作PN⊥OB于N,交CD于H,
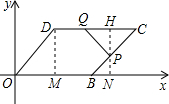
∵四邊形OBCD是平行四邊形,
∴CD=OB=8cm,BC=OD=6cm,CD∥OB,HN=DM=3

cm,
∴PH⊥CD,△CPH∽△BPN,
∴
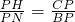
,
由題意得:PC=14-t(cm),PB=t-8(cm),CQ=t-6(cm),
∴
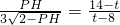
,
解得:PH=

(14-t),
∴y=S
?OBCD-S
△CPQ=8×3

-

(t-6)×

(14-t)=

t
2-5

t+45

,
∵P點越過B點在BC上運動,Q點越過C點在CD上運動,
∴8<t≤14,
∴y與t之間的函數關系式為y=

t
2-5

t+45

,t的取值范圍為8<t≤14.
分析:(1)首先過點D作DM⊥OB于M,由平行四邊形OBCD中,OB=8cm,BC=6cm,∠DOB=45°,即可求得點D的坐標,然后設經過O,B,D三點的拋物線的解析式為:y=ax(x-8),利用待定系數法即可求得經過O,B,D三點的拋物線的解析式;
(2)由平行四邊形的性質可得∠PBQ=180°-∠DOB=135°,所以若△PBQ為等腰三角形,則PB=BQ.然后設P,Q移動t秒時,△PBQ為等腰三角形,即可方程:8-t=t,解此方程即可求得答案;
(3)首先根據題意作出圖形,然后利用相似三角形的對應邊成比例,求得PH的長,又由y=S
?OBCD-S
△CPQ,即可求得y與t之間的函數關系式,由P點越過B點在BC上運動,Q點越過C點在CD上運動,即可求得t的取值范圍.
點評:此題考查了平行四邊形的性質,待定系數法求二次函數的解析式,等腰三角形的判定與性質以及多邊形面積的求解方法等知識.此題綜合性較強,難度較大,解題的關鍵是注意數形結合思想的應用,注意輔助線的作法.

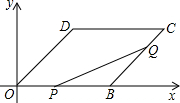 的圖形面積為y(cm2),點P,Q的移動時間為t(s),請寫出y與t之間的函數關系式,并寫出t的取值范圍.
的圖形面積為y(cm2),點P,Q的移動時間為t(s),請寫出y與t之間的函數關系式,并寫出t的取值范圍. 解:(1)過點D作DM⊥OB于M,
解:(1)過點D作DM⊥OB于M, =3
=3 ,
, ,3
,3 ),B(8,0),
),B(8,0), =3
=3 a•(3
a•(3 -8),
-8),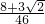 ,
,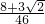 x(x-8);
x(x-8);
 cm,
cm,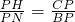 ,
,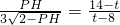 ,
, (14-t),
(14-t), -
- (t-6)×
(t-6)× (14-t)=
(14-t)= t2-5
t2-5 t+45
t+45 ,
, t2-5
t2-5 t+45
t+45 ,t的取值范圍為8<t≤14.
,t的取值范圍為8<t≤14.

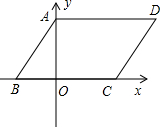 x2-7x+12=0的兩個根,且OA>OB.
x2-7x+12=0的兩個根,且OA>OB. 13、
13、 (Ⅰ)已知:如圖,平行四邊形ABCD的對角線AC、BD相交于點O,EF過點O與AB、CD分別相交于點E、F.
(Ⅰ)已知:如圖,平行四邊形ABCD的對角線AC、BD相交于點O,EF過點O與AB、CD分別相交于點E、F.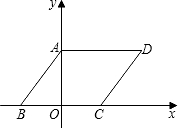 方程x2-7x+12=0的兩個根,且OA>OB;
方程x2-7x+12=0的兩個根,且OA>OB;