
【題目】某體育用品商場預測某品牌運動服能夠暢銷,就用32000元購進了一批這種運動服,上市后很快脫銷,商場又用68000元購進第二批這種運動服,所購數量是第一批購進數量的2倍,但每套進價多了10元.
(1)該商場兩次共購進這種運動服多少套?
(2)如果這兩批運動服每套的售價相同,且全部售完后總利潤不低于20%,那么每套售價至少是多少元?
科目:初中數學 來源: 題型:
【題目】一方有難八方支援,某市政府籌集抗旱必需物資120噸打算運往災區,現有甲、乙、丙三種車型可供選擇,每輛車的運載能力和運費如下表所示:(假設每輛車均滿載)

(1)若全部物資都用甲、乙兩種車來運送,需運費8200元,則分別需甲、乙兩種車各幾輛?
(2)為了節約運費,該市政府共調用16輛甲、乙,丙三種車都參與運送物資,試求出有幾種運送方案,哪種方案的運費最省?其費用是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
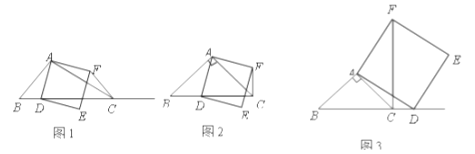
【題目】如圖1,在![]() 中,
中,![]() 為銳角,點
為銳角,點![]() 為射線
為射線![]() 上一點,聯結
上一點,聯結![]() ,以
,以![]() 為一邊且在
為一邊且在![]() 的右側作正方形
的右側作正方形![]() .
.
(1)如果![]() ,
,![]() ,
,
①當點![]() 在線段
在線段![]() 上時(與點
上時(與點![]() 不重合),如圖2,線段
不重合),如圖2,線段![]() 所在直線的位置關系為 ,線段
所在直線的位置關系為 ,線段![]() 的數量關系為 ;
的數量關系為 ;
②當點![]() 在線段
在線段![]() 的延長線上時,如圖3,①中的結論是否仍然成立,并說明理由;
的延長線上時,如圖3,①中的結論是否仍然成立,并說明理由;
(2)如果![]() ,
,![]() 是銳角,點
是銳角,點![]() 在線段
在線段![]() 上,當
上,當![]() 滿足什么條件時,
滿足什么條件時,![]() (點
(點![]() 不重合),并說明理由.
不重合),并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用四個螺絲將四條不可彎曲的本條圍成一個木框(形狀不限),不記螺絲大小,其中相鄰兩螺絲之間的距離依次為3,4,5,7.且相鄰兩本條的夾角均可調整,若調整木條的夾角時不破壞此木框,則任意兩個螺絲之間的最大距離是( )
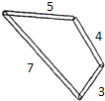
A.6B.7C.8D.9
查看答案和解析>>
科目:初中數學 來源: 題型:
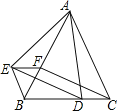
【題目】如圖,△ABC和△BEF都是等邊三角形,點D在BC邊上,點F在AB邊上,且∠EAD=60°,連接ED、CF.
(1)求證:△ABE≌△ACD;
(2)求證:四邊形EFCD是平行四邊形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,并解決后面的問題.
材料:一般地,![]() 個相同的因數
個相同的因數![]() 相乘:
相乘:![]() 個
個![]() 記為
記為![]() ,如
,如![]() ,此時,3叫做以2為底8的對數,記為
,此時,3叫做以2為底8的對數,記為![]() (即
(即![]() ).
).
一般地,若![]() (
(![]() 且
且![]() ,
,![]() ),則
),則![]() 叫做以
叫做以![]() 為底
為底![]() 的對數,記為
的對數,記為![]() (即
(即![]() ).如
).如![]() ,則4叫做以3為底81的對數,記為
,則4叫做以3為底81的對數,記為![]() (即
(即![]() ).
).
問題:(1)計算以下各對數的值:![]() ________,
________,![]() ________,
________,![]() ________.
________.
(2)觀察(1)中三數4、16、64之間滿足怎樣的關系式?![]() 、
、![]() 、
、![]() 之間又滿足怎樣的關系式?______________________________________________________________________________
之間又滿足怎樣的關系式?______________________________________________________________________________
(3)由(2)的結果,你能歸納出一個一般性的結論嗎?
![]() ____________________(
____________________(![]() 且
且![]() ,
,![]() ,
,![]() )
)
(4)根據冪的運算法則:![]() 以及對數的含義證明(3)中結論.
以及對數的含義證明(3)中結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為準備參加某市2019年度中小學生機器人競賽,學校對甲、乙兩支機器人制作小隊所創作的機器人分別從創意、設計、編程與制作三方面進行量化,各項量化滿分100分,根據量化結果擇優推薦.它們三項量化得分如下表:
量化項目 | 量化得分 | |
甲隊 | 乙隊 | |
創意 | 85 | 72 |
設計 | 70 | 66 |
編程與制作 | 64 | 84 |
(1)如果根據三項量化的平均分擇優推薦,哪隊將被推薦參賽?
(2)根據本次中小學生機器人競賽的主題要求,如果學校根據創意、設計、編程與制作三項量化得分按![]() 的比例確定每隊最后得分的平均分擇優推薦,哪隊將被推薦參賽?并對另外一隊提出合理化的建議.
的比例確定每隊最后得分的平均分擇優推薦,哪隊將被推薦參賽?并對另外一隊提出合理化的建議.
查看答案和解析>>
科目:初中數學 來源: 題型:
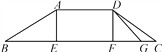
【題目】為了方便行人,市政府打算修建如圖所示的過街天橋,橋面AD平行于地面BC,立柱AE⊥BC于點E,立柱DF⊥BC于點F,若AB=5![]() 米,tanB=
米,tanB=![]() ,∠C=30°.
,∠C=30°.
(1)求橋面AD與地面BC之間的距離.
(2)因受地形限制,決定對該天橋進行改建,使CD斜面的坡度變陡,將其30°坡角改為40°,改建后斜面為DG,試計算此次改建節省路面寬度CG大約應是多少?(結果精確到0.1米,參考數據:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com