
【題目】某商店銷售![]() 型和
型和![]() 型兩種學習機,其中用10000元采購
型兩種學習機,其中用10000元采購![]() 型學習機臺數和用8000元采購
型學習機臺數和用8000元采購![]() 型學習機臺數相等,且一臺
型學習機臺數相等,且一臺![]() 型學習機比一臺
型學習機比一臺![]() 型學習機進價多100元.
型學習機進價多100元.
(1)求一臺![]() 型和
型和![]() 型學習機價格各是多少元?
型學習機價格各是多少元?
(2)若購進![]() 型學習機共100臺,其中
型學習機共100臺,其中![]() 型的進貨量不超過
型的進貨量不超過![]() 型的2倍,設購進
型的2倍,設購進![]() 型學習機
型學習機![]() 臺.
臺.
①求![]() 的取值范圍.
的取值范圍.
②已知![]() 型學習機售價均是900元/臺,實際進貨時,廠家對
型學習機售價均是900元/臺,實際進貨時,廠家對![]() 型學習機在原進貨價的基礎,上下調
型學習機在原進貨價的基礎,上下調![]() 元,且限定商店最多購進
元,且限定商店最多購進![]() 型學習機60臺,若商店保持同種學習機的售價不變,請你根據以上信息,求出使這100臺學習機銷售總利潤
型學習機60臺,若商店保持同種學習機的售價不變,請你根據以上信息,求出使這100臺學習機銷售總利潤![]() (元)的最大值.
(元)的最大值.
【答案】(1)![]() 型進價每臺500元,
型進價每臺500元,![]() 型進價每臺400元
型進價每臺400元
(2)①![]() ;
;
②當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;當
;當![]() 時,
時, ![]()
【解析】
(1)根據“用10000元采購![]() 型學習機臺數和用8000元采購
型學習機臺數和用8000元采購![]() 型學習機臺數相等”,列分式方程求解即可;
型學習機臺數相等”,列分式方程求解即可;
(2)①根據條件中可以列出關于![]() 的不等式組,求
的不等式組,求![]() 的取值范圍;
的取值范圍;
②本問中,首先根據題意,可以先列出銷售利潤![]() 與
與![]() 的函數關系,通過討論所含字母
的函數關系,通過討論所含字母![]() 的取值范圍,得到
的取值范圍,得到![]() 與
與![]() 的函數關系.
的函數關系.
(1)設![]() 型進價每臺
型進價每臺![]() 元,
元,![]() 型進價每臺
型進價每臺![]() 元,則
元,則
![]()
解得:![]()
經檢驗![]() 是原方程的解且符合題意,
是原方程的解且符合題意,
![]()
答:![]() 型進價每臺500元,
型進價每臺500元,![]() 型進價每臺400元
型進價每臺400元
(2)①根據題意可得:![]()
解得:![]()
![]() 為正整數,
為正整數,
![]()
②根據題意,得![]()
即![]()
(1)當![]() 時,
時,![]() 的值隨
的值隨![]() 值的增大而減小
值的增大而減小
![]() 當
當![]() 時,
時,![]() ,
,
(2)當![]() 時,
時,![]() ,
,![]() ;
;
(3)當![]() 時,
時,![]() ,
, ![]() 的值隨
的值隨![]() 值的增大而增大
值的增大而增大
![]() 當
當![]() 時,
時, ![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖在平面直角坐標系中,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與反比例函數
,與反比例函數![]() 在第二象限內的圖象相交于點
在第二象限內的圖象相交于點![]() .
.
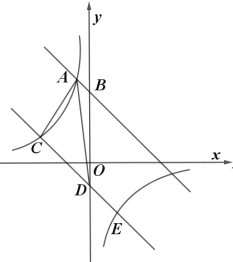
![]() 求直線
求直線![]() 的解析式;
的解析式;
![]() 將直線
將直線![]() 向下平移
向下平移![]() 個單位后與反比例函數的圖象交于點
個單位后與反比例函數的圖象交于點![]() 和點
和點![]() 與
與![]() 軸交于點
軸交于點![]() 求
求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]() (
(![]() 為常數)的頂點為
為常數)的頂點為![]() .
.
(1)求點![]() 的坐標;(用含
的坐標;(用含![]() 的式子表示)
的式子表示)
(2)在同一平面直角坐標系中,存在函數圖象![]() ,點
,點![]() 在圖象
在圖象![]() 上,點
上,點![]() 在拋物線
在拋物線![]() 上,對于任意的實數
上,對于任意的實數![]() ,都有點
,都有點![]() ,
,![]() 關于點
關于點![]() 對稱.
對稱.
①當![]() 時,求圖象
時,求圖象![]() 對應函數的解析式;
對應函數的解析式;
②當![]() 時,都有
時,都有![]() 成立,結合圖象,求
成立,結合圖象,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,點
,點![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,![]() 點在邊
點在邊![]() 上,連接
上,連接![]() ,過點
,過點![]() 作
作![]() 的垂線交
的垂線交![]() 于點
于點![]() ,垂足為點
,垂足為點![]() ,且
,且![]() 與四邊形
與四邊形![]() 的周長相等,設
的周長相等,設![]() ,
,![]() .
.
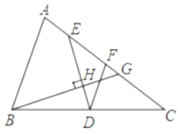
(1)求證:![]() ;
;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于一個函數,自變量x取a時,函數值y也等于a,我們稱a為這個函數的不動點.如果二次函數y=x2+2x+c有兩個相異的不動點x1、x2,且x1<1<x2,則c的取值范圍是( )
A. c<﹣3B. c<﹣2C. c<![]() D. c<1
D. c<1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一道滿分3分的數學測驗題,網絡閱卷時老師評分只能給整數,即得分可能為0分,1分,2分,3分.為了解學生知識點掌握情況及試題的難易程度,對初三(1)班所有學生的這道試題得分情況進行分析整理后,繪制了兩幅尚不完整的統計圖,如圖所示.
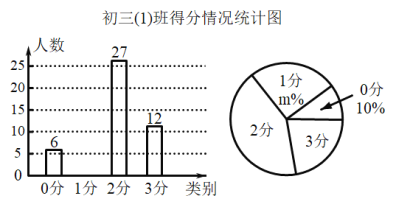

根據以上信息,解答下列問題:
(1)m= ,得分為“3分”對應的扇形圓心角為 度,請補全條形統計圖;
(2)由“小知識”提供的信息,請依據計算得到的L的值,判斷這道題屬于哪一類難度的試題?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,平面直角坐標系xOy中,矩形ABCD的邊AB=4,BC=6.在不改變矩形ABCD的形狀和大小的情況下,當矩形的頂點A在x軸的正半軸上左右移動時,另一個頂點D始終在y軸的正半軸上隨之上下移動.
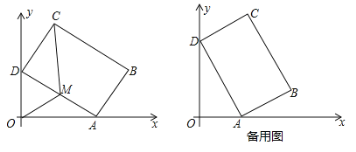
(1)當∠OAD=30°時,求點C的坐標;
(2)設AD的中點為M,連接OM、MC,若四邊形OMCD的面積為![]() 時,求OA的長;
時,求OA的長;
(3)在點A移動過程中是否存在某一位置,使點C到點O的距離有最大值?若存在,求此時的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了加快“智慧校園”建設,某市準備為試點學校采購一批![]() 、
、![]() 兩種型號的一體機,經過市場調查發現,今年每套
兩種型號的一體機,經過市場調查發現,今年每套![]() 型一體機的價格比每套
型一體機的價格比每套![]() 型一體機的價格多0.6萬元,且用960萬元恰好能購買500套
型一體機的價格多0.6萬元,且用960萬元恰好能購買500套![]() 型一體機和200套
型一體機和200套![]() 型一體機.
型一體機.
(1)求今年每套![]() 型、
型、![]() 型一體機的價格各是多少萬元
型一體機的價格各是多少萬元
(2)該市明年計劃采購![]() 型、
型、![]() 型一體機1100套,考慮物價因素,預計明年每套
型一體機1100套,考慮物價因素,預計明年每套![]() 型一體機的價格比今年上漲25%,每套
型一體機的價格比今年上漲25%,每套![]() 型一體機的價格不變,若購買
型一體機的價格不變,若購買![]() 型一體機的總費用不低于購買
型一體機的總費用不低于購買![]() 型一體機的總費用,那么該市明年至少需要投入多少萬元才能完成采購計劃?
型一體機的總費用,那么該市明年至少需要投入多少萬元才能完成采購計劃?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() ,
,![]() ,
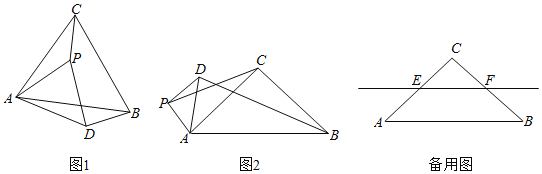
,![]() .點P是平面內不與點A,C重合的任意一點.連接AP,將線段AP繞點P逆時針旋轉α得到線段DP,連接AD,BD,CP.
.點P是平面內不與點A,C重合的任意一點.連接AP,將線段AP繞點P逆時針旋轉α得到線段DP,連接AD,BD,CP.
(1)觀察猜想
如圖1,當![]() 時,
時,![]() 的值是 ,直線BD與直線CP相交所成的較小角的度數是 .
的值是 ,直線BD與直線CP相交所成的較小角的度數是 .
(2)類比探究
如圖2,當![]() 時,請寫出
時,請寫出![]() 的值及直線BD與直線CP相交所成的小角的度數,并就圖2的情形說明理由.
的值及直線BD與直線CP相交所成的小角的度數,并就圖2的情形說明理由.
(3)解決問題
當![]() 時,若點E,F分別是CA,CB的中點,點P在直線EF上,請直接寫出點C,P,D在同一直線上時
時,若點E,F分別是CA,CB的中點,點P在直線EF上,請直接寫出點C,P,D在同一直線上時![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com