【答案】
分析:①∠AED=90°-∠EAD,∠ADC=90°-∠DAC,∠EAD=∠DAC;
②易證△ADE∽△ACD,得DE:DA=DC:AC=1:AC,AC不一定等于2;
③當FC⊥AB時成立;
④連接DM,可證DM∥BF∥AC,得FM:MC=BD:DC=4:3;易證△FMB∽△CMA,得比例線段求解;
⑤BE=DE成立.由④可知BM:MA=BF:AC=2:1,而BD:DC=2:1,可知DM∥AC,DM⊥BC,利用直角三角形斜邊上的中線的性質判斷.
解答:解:①∠AED=90°-∠EAD,∠ADC=90°-∠DAC,
∵∠EAD=∠DAC,
∴∠AED=∠ADC.
故本選項正確;
②∵∠EAD=∠DAC,∠ADE=∠ACD=90°,
∴△ADE∽△ACD,得DE:DA=DC:AC=3:AC,但AC的值未知,
故不一定正確;
③由①知∠AED=∠ADC,
∴∠BED=∠BDA,
又∵∠DBE=∠ABD,
∴△BED∽△BDA,
∴DE:DA=BE:BD,由②知DE:DA=DC:AC,
∴BE:BD=DC:AC,
∴AC•BE=BD•DC=2.
故本選項正確;
④連接DM.
在Rt△ADE中,MD為斜邊AE的中線,則DM=MA.
∴∠MDA=∠MAD=∠DAC,
∴DM∥BF∥AC,
由DM∥BF得FM:MC=BD:DC=2:1;
由BF∥AC得△FMB∽△CMA,有BF:AC=FM:MC=2:1,
∴BF=2AC.
故本選項正確
⑤由④可知BM:MA=BF:AC=2:1,
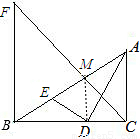
∵BD:DC=2:1,∴DM∥AC,DM⊥BC,
∴∠MDA=∠DAC=∠DAM,而∠ADE=90°,
∴DM=MA=ME,在Rt△BDM中,由BM=2AM可知BE=EM,
∴ED=BE.故⑤正確.
綜上所述,①③④⑤正確,共有4個.
故選D.
點評:此題重點考查相似三角形的判定和性質,綜合性強,有一定難度.

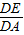 =
= ;③AC•BE=2;④BF=2AC;⑤BE=DE
;③AC•BE=2;④BF=2AC;⑤BE=DE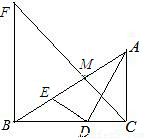



 A加金題 系列答案
A加金題 系列答案 全優測試卷系列答案
全優測試卷系列答案
 如圖,Rt△ABC中,∠ACB=90°,tanB=
如圖,Rt△ABC中,∠ACB=90°,tanB= 如圖,Rt△ABC中,∠C=90°,△ABC的內切圓⊙0與BC、CA、AB分別切于點D、E、F.
如圖,Rt△ABC中,∠C=90°,△ABC的內切圓⊙0與BC、CA、AB分別切于點D、E、F.