
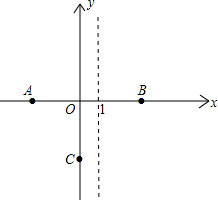 拋物線y=ax2+bx+c交x軸于A、B兩點,交y軸于點C,已知拋物線的對稱軸為x=1,B(3,0),C(0,-3),
拋物線y=ax2+bx+c交x軸于A、B兩點,交y軸于點C,已知拋物線的對稱軸為x=1,B(3,0),C(0,-3), 解:(1)將C(0,-3)代入y=ax2+bx+c,
解:(1)將C(0,-3)代入y=ax2+bx+c, .(2)
.(2) =1,
=1, ,
, (舍去),
(舍去),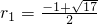 ,
, (舍去).
(舍去).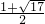 或
或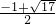 .
. =1,然后可將B點坐標代入拋物線的解析式中,聯立由對稱軸得出的關系式即可求出拋物線的解析式.
=1,然后可將B點坐標代入拋物線的解析式中,聯立由對稱軸得出的關系式即可求出拋物線的解析式.

科目:初中數學 來源: 題型:
| MN•OP | MN+OP |

查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•陜西)如果一條拋物線y=ax2+bx+c(a≠0)與x軸有兩個交點,那么以該拋物線的頂點和這兩個交點為頂點的三角形稱為這條拋物線的“拋物線三角形”.
(2012•陜西)如果一條拋物線y=ax2+bx+c(a≠0)與x軸有兩個交點,那么以該拋物線的頂點和這兩個交點為頂點的三角形稱為這條拋物線的“拋物線三角形”.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com