把拋物線y=2x2-4x-5繞頂點旋轉180°,得到的新拋物線的解析式是( )
A.y=-2x2-4x-5
B.y=-2x2+4x+5
C.y=-2x2+4x-9
D.以上都不對
【答案】
分析:易得拋物線的頂點,由于是繞頂點旋轉,所以新拋物線的頂點不變,得到原拋物線上的一點繞頂點旋轉180°后得到的坐標,代入用頂點表示的新拋物線求解析式即可.
解答: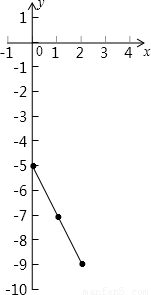
解:y=2x
2-4x-5=2(x-1)
2-7,
∴原拋物線的頂點為(1,-7),
點(0,-5)在原拋物線上.
由圖中可得(0,-5)繞頂點(1,-7)旋轉180°后得到點的坐標為(2,-9).
設新拋物線的解析式為y=a(x-1)
2-7,
把(2,-9)代入新拋物線可得a=-2,
∴新拋物線的解析式為y=-2(x-1)
2-7=-2x
2+4x-9,故選C.
點評:考查二次函數的幾何變換問題;得到新函數的頂點及一點是解決本題的關鍵.

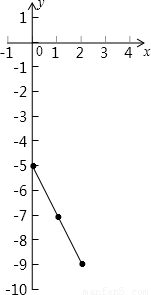 解:y=2x2-4x-5=2(x-1)2-7,
解:y=2x2-4x-5=2(x-1)2-7,
