
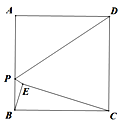
【題目】如圖,正方形ABCD的邊長為6,點E是正方形內部一點,連接BE,CE,且∠ABE=∠BCE,點P是邊AB上一動點,連接PD,PE,則PD+PE的最小值為_____.
【答案】![]()
【解析】
根據正方形的性質得到∠ABC=90°,推出∠BEC=90°,得到點E在以BC為直徑的半圓上移動,如圖,設BC的中點為O,作正方形ABCD關于直線AB對稱的正方形AFGB,則點D的對應點是F,連接FO交AB于P,交⊙O于E,則線段EF的長即為PD+PE的長度最小值,根據勾股定理即可得到結論.
解:∵四邊形ABCD是正方形,
∴∠ABC=90°,
∴∠ABE+∠CBE=90°,
∵∠ABE=∠BCE,
∴∠BCE+∠CBE=90°,
∴∠BEC=90°,
∴點E在以BC為直徑的半圓上移動,
如圖,設BC的中點為O,
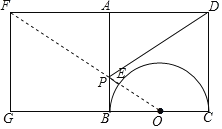
作正方形ABCD關于直線AB對稱的正方形AFGB,
則點D的對應點是F,
連接FO交AB于P,交半圓O于E,
則線段EF的長即為PD+PE的長度最小值,
∵∠G=90°,FG=BG=AB=6,
∴OG=9,
∴OF=![]() =
=![]() ,
,
∴EF=![]() ,
,
故PD+PE的長度最小值為![]() ,
,
故答案為:![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
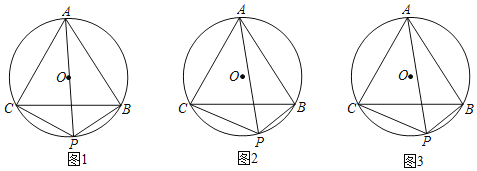
【題目】如圖,△ABC是⊙O的內接正三角形,點P在劣弧BC上(不與點B,C重合).
(1)如圖1,若PA是⊙O的直徑,則PA______PB+PC(請填“>”,“=”或“<”)
(2)如圖2,若PA不是⊙O的直徑,那么(1)中的結論是否仍成立?如果不成立,請說明理由:如果成立,請給出證明.
(3)如圖3,若四邊形ACPB的面積是16![]() .
.
①求PA的長;
②設y=S△PCB+![]() S△PCA,求當PC為何值時,y的值最大?并直接寫出此時⊙O的半徑.
S△PCA,求當PC為何值時,y的值最大?并直接寫出此時⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將兩個全等的直角三角形ABC和DBE按圖![]() 方式擺放,其中
方式擺放,其中![]() ,
,![]() ,點E落在AB上,DE所在直線交AC所在直線于點F.
,點E落在AB上,DE所在直線交AC所在直線于點F.
![]() 求證:
求證:![]() ;
;
![]() 若將圖
若將圖![]() 中的
中的![]() 繞點B按順時針方向旋轉角a,且
繞點B按順時針方向旋轉角a,且![]() ,其他條件不變,如圖
,其他條件不變,如圖![]() 請你直接寫出
請你直接寫出![]() 與DE的大小關系:
與DE的大小關系:![]() ______
______![]() 填“
填“![]() ”或“
”或“![]() ”或“
”或“![]() ”
”![]()
![]() 若將圖
若將圖![]() 中
中![]() 的繞點B按順時針方向旋轉角
的繞點B按順時針方向旋轉角![]() ,且
,且![]() ,其他條件不變,如圖
,其他條件不變,如圖![]() 請你寫出此時AF、EF與DE之間的關系,并加以證明.
請你寫出此時AF、EF與DE之間的關系,并加以證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,射線AP交⊙O于C點,∠PCO的平分線交⊙O于D點,過點D作![]() 交AP于E點.
交AP于E點.
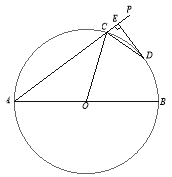
(1)求證:DE為⊙O的切線;
(2)若DE=3,AC=8,求直徑AB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
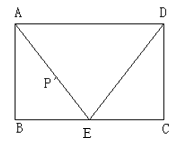
【題目】已知矩形![]() 中,
中,![]() 米,
米,![]() 米,
米,![]() 為
為![]() 中點,動點
中點,動點![]() 以2米/秒的速度從
以2米/秒的速度從![]() 出發,沿著
出發,沿著![]() 的邊,按照A
的邊,按照A![]() E
E![]() D
D![]() A順序環行一周,設
A順序環行一周,設![]() 從
從![]() 出發經過
出發經過![]() 秒后,
秒后,![]() 的面積為
的面積為![]() (平方米),求
(平方米),求![]() 與
與![]() 間的函數關系式.
間的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有長為24m的籬笆,現一面利用墻(墻的最大可用長度a為10m)圍成中間隔有一道籬笆的長方形花圃,設花圃的寬AB為xm,面積為Sm2.
(1)求S與x的函數關系式及x值的取值范圍;
(2)要圍成面積為45m2的花圃,AB的長是多少米?
(3)當AB的長是多少米時,圍成的花圃的面積最大?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明袋子中有1個紅球和n個白球,這些球除顏色外無其他差別.
(1)從袋中隨機摸出一個球,記錄其顏色,然后放回.大量重復該實驗,發現摸到紅球的頻率穩定于0.25,求n的值.
(2)在(1)的條件下,從袋中隨機摸出兩個球,求兩個球顏色不同的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】雜技團進行雜技表演,演員從蹺蹺板右端A處彈跳到人梯頂端椅子B處,其身體(看成一點)的路線是拋物線![]() 的一部分,如圖
的一部分,如圖
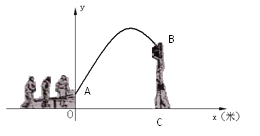
(1)求演員彈跳離地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳點A的水平距離是4米,問這次表演是否成功?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知長方形![]() 中,
中,![]() ,點
,點![]() 在邊
在邊![]() 上,由
上,由![]() 往
往![]() 運動,速度為
運動,速度為![]() ,運動時間為
,運動時間為![]() 秒,將
秒,將![]() 沿著
沿著![]() 翻折至
翻折至![]() ,點
,點![]() 對應點為
對應點為![]() ,
,![]() 所在直線與邊
所在直線與邊![]() 交與點
交與點![]() ,
,
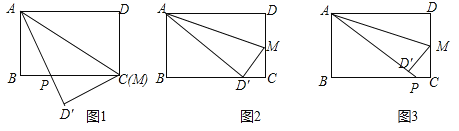
(1)如圖![]() ,當
,當![]() 時,求證:
時,求證:![]() ;
;
(2)如圖![]() ,當
,當![]() 為何值時,點
為何值時,點![]() 恰好落在邊
恰好落在邊![]() 上;
上;
(3)如圖![]() ,當
,當![]() 時,求
時,求![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com