
【題目】如圖,Rt△CEF中,∠C=90°,∠CEF, ∠CFE外角平分線交于點A,過點A分別作直線CE、CF的垂線,B、D為垂足.
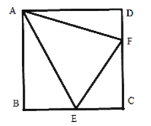
(1)求證:四邊形ABCD是正方形,
(2)已知AB的長為6,求(BE+6)(DF+6)的值,
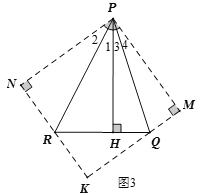
(3)借助于上面問題的解題思路,解決下列問題:若三角形PQR中,∠QPR=45°,一條高是PH,長度為6,QH=2,則HR= .
【答案】(1)見解析;(2)72;(3)3.
【解析】
(1)根據(jù)三個角是直角的四邊形先證得四邊形ABCD是矩形,再過點A作AG⊥EF于點G,根據(jù)角平分線的性質(zhì)得出AB=AG= AD,問題即得解決;
(2)如圖1,通過兩次運用HL可證得EF=BE+DF,再設(shè)BE=x,DF=y,在Rt△CEF中,根據(jù)勾股定理得出關(guān)于x、y的等式,再整體代入![]() 展開整理后的式子即可得到答案;
展開整理后的式子即可得到答案;
(3)如圖3,作△PRH關(guān)于PR對稱的△PRN,作△PQH關(guān)于PQ對稱的△PQM,NR和MQ的延長線交于點K,先根據(jù)鄰邊相等的矩形是正方形證明四邊形PNKM是正方形,再根據(jù)(2)的結(jié)論即可求出結(jié)果.
解:(1)證明:∵AD⊥CD,AB⊥CB,∠C=90°,
∴四邊形ABCD是矩形,
如圖1,過點A作AG⊥EF于點G,
∵AF平分∠DFE,AD⊥CD,
∴AG=AD,
同理可得:AG=AB,
∴AB=AD.
∴矩形ABCD是正方形.
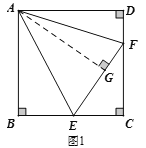
(2)在Rt△ADF和Rt△AGF中,
![]()
∴Rt△ADF≌Rt△AGF(HL).
∴DF=GF,
同理可得BE=GE.
∴EF=GE+GF=BE+DF.
設(shè)BE=EG=x,DF=FG=y,則CE=6-x,CF=6-y,如圖2:

在Rt△CEF中,根據(jù)勾股定理得:![]() ,即
,即![]() ,整理得:
,整理得:![]() .
.
∴![]() .
.
(3)如圖3,作△PRH關(guān)于PR對稱的△PRN,作△PQH關(guān)于PQ對稱的△PQM,NR和MQ的延長線交于點K,則PN=PH=6,PM=PH=6,∠2=∠1,∠4=∠3,∠N=∠PHR=90°,∠M=∠PHQ=90°,MQ=HQ=2,NR=HR,
∴PN=PM=6,
∵∠1+∠3=45°,
∴∠1+∠2+∠3+∠4=90°,即∠NPM=90°,
∴四邊形PNKM是正方形.
∵RQ=RH+HQ=NR+QM,
∴由(2)題的結(jié)論知:![]() ,
,
即![]() ,解得
,解得![]() ,即HR=3.
,即HR=3.
故答案為3.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1在△ABC中,∠ACB=90°,AC=BC,直線MN經(jīng)過點C,且AD⊥MN于點D,BE⊥MN于點E.
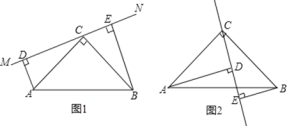
(1)求證:①△ADC≌△CEB;②DE=AD+BE.
(2)當直線MN繞點C旋轉(zhuǎn)到圖2的位置時,DE、AD、BE又怎樣的關(guān)系?并加以證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
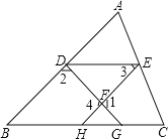
【題目】如圖:點D、E、H、G分別在△ABC的邊上DE∥BC,∠3=∠B,DG、EH交于點F.求證:∠1+∠2=180°
證明:(請將下面的證明過程補充完整)
∵DE∥BC(已知)
∴∠3=∠EHC(______)
∵∠3=∠B(已知)
∴∠B=∠EHC(______)
∴AB∥EH(______)
∴∠2+∠______=180°(______)
∵∠1=∠4(______)
∴∠1+∠2=180°(等量代換)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC內(nèi)接于⊙O,∠CBG=∠A,CD為直徑,OC與AB相交于點E,過點E作EF⊥BC,垂足為F,延長CD交GB的延長線于點P,連接BD.
(1)求證:PG與⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的條件下,若⊙O的半徑為8,PD=OD,求OE的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖,點P在線段AB外,且PA=PB,求證:點P在線段AB的垂直平分線上,在證明該結(jié)論時,需添加輔助線,則作法不正確的是( )

A. 作∠APB的平分線PC交AB于點C
B. 過點P作PC⊥AB于點C且AC=BC
C. 取AB中點C,連接PC
D. 過點P作PC⊥AB,垂足為C
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,∠E=∠F=90°,∠B=∠C,AE=AF,下列結(jié)論不正確的結(jié)論是( )
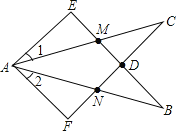
A.CD=DN;B.∠1=∠2;C.BE=CF;D.△ACN≌△ABM.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,已知AB=AC,D為∠BAC的角平分線上面一點,連接BD,CD;如圖2,已知AB=AC,D、E為∠BAC的角平分線上面兩點,連接BD,CD,BE,CE;如圖3,已知AB=AC,D、E、F為∠BAC的角平分線上面三點,連接BD,CD,BE,CE,BF,CF;…,依次規(guī)律,第n個圖形中有全等三角形的對數(shù)是_________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 厘米,
厘米,![]() ,
,![]() 厘米,點
厘米,點![]() 為
為![]() 的中點,如果點
的中點,如果點![]() 在線段
在線段![]() 上以
上以![]() 厘米/秒的速度由點向點運動,同時點
厘米/秒的速度由點向點運動,同時點![]() 在線段
在線段![]() 上由
上由![]() 點向
點向![]() 點運動.當一個點停止運動時,另一個點也隨之停止運動.
點運動.當一個點停止運動時,另一個點也隨之停止運動.

(1)用含有![]() 的代數(shù)式表示
的代數(shù)式表示![]() ,則
,則![]() _______厘米;
_______厘米;
(2)若點![]() 的運動速度與點
的運動速度與點![]() 的運動速度相等,經(jīng)過
的運動速度相等,經(jīng)過![]() 秒后,
秒后,![]() 與
與![]() 是否全等,請說明理由;
是否全等,請說明理由;
(3)若點![]() 的運動速度與點
的運動速度與點![]() 的運動速度不相等,那么當點
的運動速度不相等,那么當點![]() 的運動速度為多少時,能夠使
的運動速度為多少時,能夠使![]() 與
與![]() 全等?
全等?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
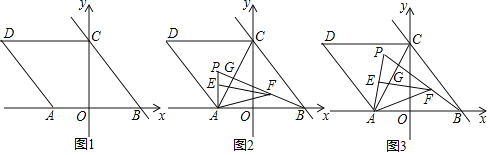
【題目】已知:在平面直角坐標系中,點O為坐標原點,點A在x軸的負半軸上,直線y=﹣![]() x+
x+![]() 與x軸、y軸分別交于B、C兩點,四邊形ABCD為菱形.
與x軸、y軸分別交于B、C兩點,四邊形ABCD為菱形.
(1)如圖1,求點A的坐標;
(2)如圖2,連接AC,點P為△ACD內(nèi)一點,連接AP、BP,BP與AC交于點G,且∠APB=60°,點E在線段AP上,點F在線段BP上,且BF=AE,連接AF、EF,若∠AFE=30°,求AF2+EF2的值;
(3)如圖3,在(2)的條件下,當PE=AE時,求點P的坐標.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com