
【題目】如圖,在![]() 中,
中,![]() ,以
,以![]() 為直徑作⊙
為直徑作⊙![]() ,在⊙
,在⊙![]() 上一點
上一點![]() ,
,![]() .
.

(1)求證:![]() 是⊙
是⊙![]() 的切線;
的切線;
(2)過![]() 作
作![]() 分別與
分別與![]() 、
、![]() 和⊙
和⊙![]() 交于點
交于點![]() 、
、![]() 、
、![]() ,若
,若![]() ,
,![]() .
.
①求⊙![]() 的半徑長;
的半徑長;
②直接寫出![]() 的長.
的長.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】某醫院醫生為了研究該院某種疾病的診斷情況,需要調查來院就診的病人的兩個生理指標![]() ,
,![]() ,于是他分別在這種疾病的患者和非患者中,各隨機選取20人作為調查對象,將收集到的數據整理后,繪制統計圖如下:
,于是他分別在這種疾病的患者和非患者中,各隨機選取20人作為調查對象,將收集到的數據整理后,繪制統計圖如下:
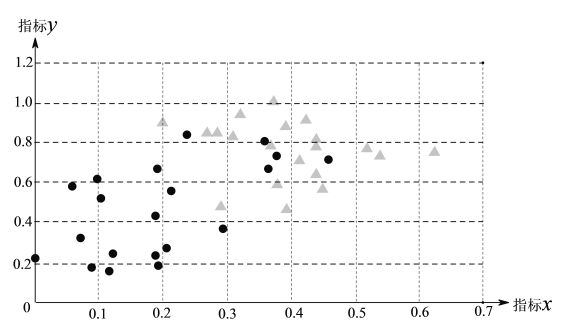
注“●”表示患者,“▲”表示非患者.
根據以上信息,回答下列問題:
(1)在這40名被調查者中,
①指標![]() 低于0.4的有 人;
低于0.4的有 人;
②將20名患者的指標![]() 的平均數記作
的平均數記作![]() ,方差記作
,方差記作![]() ,20名非患者的指標
,20名非患者的指標![]() 的平均數記作
的平均數記作![]() ,方差記作
,方差記作![]() ,則
,則![]()
![]() ,
,![]()
![]() (填“>”,“=”或“<”);
(填“>”,“=”或“<”);
(2)來該院就診的500名未患這種疾病的人中,估計指標![]() 低于0.3的大約有 人;
低于0.3的大約有 人;
(3)若將“指標![]() 低于0.3,且指標
低于0.3,且指標![]() 低于0.8”作為判斷是否患有這種疾病的依據,則發生漏判的概率多少.
低于0.8”作為判斷是否患有這種疾病的依據,則發生漏判的概率多少.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,半徑為2的
,半徑為2的![]() 從點
從點![]() 開始(如圖①)沿直線
開始(如圖①)沿直線![]() 向右滾動,滾動時始終與直線
向右滾動,滾動時始終與直線![]() 相切(切點為
相切(切點為![]() ),當
),當![]() 與
與![]() 只有一個公共點時滾動停止.作
只有一個公共點時滾動停止.作![]() 于點
于點![]() .
.
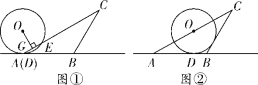
(1)圖①中,![]() 在
在![]() 邊上截得的弦長
邊上截得的弦長![]() ______;
______;
(2)當圓心落在![]() 上時,如圖②,判斷
上時,如圖②,判斷![]() 與
與![]() 的位置關系,請說明理由;
的位置關系,請說明理由;
(3)在![]() 滾動過程中,線段
滾動過程中,線段![]() 的長度隨之變化,設
的長度隨之變化,設![]() ,
,![]() ,求出
,求出![]() 與
與![]() 之間的函數關系式,并直接寫出
之間的函數關系式,并直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
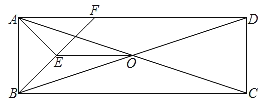
【題目】如圖,ABCD的對角線AC,BD相交于點O.E,F是AC上的兩點,并且AE=CF,連接DE,BF.
(1)求證:△DOE≌△BOF;
(2)若BD=EF,連接DE,BF.判斷四邊形EBFD的形狀,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一組正方形按如圖所示的方式放置,其中頂點B1在y軸上,頂點C1,E1,E2,C2,E3,E4,C3……在x軸上,已知正方形A1B1C1D1的邊長為1,∠B1C1O=60°,B1C1∥B2C2∥B3C3……,則正方形A2020B2020C2020D2020的邊長是( )
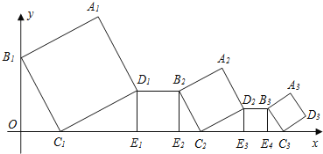
A.(![]() )2017B.(
)2017B.(![]() )2018C.(
)2018C.(![]() )2019D.(
)2019D.(![]() )2020
)2020
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線![]() 分別與x軸、y軸相交于點B、C,經過點B、C的拋物線
分別與x軸、y軸相交于點B、C,經過點B、C的拋物線![]() 與x軸的另一個交點為A(-1,0).
與x軸的另一個交點為A(-1,0).
(1)求這個拋物線的表達式;
(2)已知點D在拋物線上,且橫坐標為2,求出△BCD的面積;
(3)點P是直線BC上方的拋物線上一動點,過點P作PQ垂直于x軸,垂足為Q.是否存在點P,使得以點A、P、Q為頂點的三角形與△BOC相似?若存在,請求出點P的坐標;若不存在,請說明理由.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,對角線AC與BD相交于點O,F為DA上一點,連接BF,E為BF中點,CD=6,sin∠ADB=![]() ,若△AEF的周長為18,則S△BOE=_____.
,若△AEF的周長為18,則S△BOE=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】[問題提出]
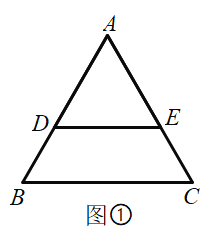
(1)如圖![]() 均為等邊三角形,點
均為等邊三角形,點![]() 分別在邊
分別在邊![]() 上.將
上.將![]() 繞點
繞點![]() 沿順時針方向旋轉,連結
沿順時針方向旋轉,連結![]() .在圖
.在圖![]() 中證明
中證明![]() .
.

[學以致用]
(2)在![]() 的條件下,當點
的條件下,當點![]() 在同一條直線上時,
在同一條直線上時,![]() 的大小為 度.
的大小為 度.
[拓展延伸]
(3)在![]() 的條件下,連結
的條件下,連結![]() .若
.若![]() 直接寫出
直接寫出![]() 的面積
的面積![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com