(1)證明:如圖,設F為AD延長線上一點,
∵A,B,C,D四點共圓,
∴∠CDF=∠ABC,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ADB=∠ACB,
∴∠ADB=∠CDF,
∵∠ADB=∠EDF(對頂角相等),
∴∠EDF=∠CDF,
即AD的延長線平分∠CDE.
(2)解:設O為外接圓圓心,連接AO比延長交BC于H,連接OC,
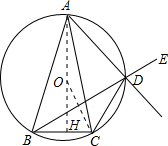
∵AB=AC,
∴

=

,
∴AH⊥BC,
∴∠OAC=∠OAB=

∠BAC=

×30°=15°,
∴∠COH=2∠OAC=30°,
設圓半徑為r,
則OH=OC•cos30°=

r,
∵△ABC中BC邊上的高為1,
∴AH=OA+OH=r+

r=1,
解得:r=2(2-

),
∴△ABC的外接圓的面積為:4π(2-

).
分析:(1)要證明AD的延長線平分∠CDE,即證明∠EDF=∠CDF,轉化為證明∠ADB=∠CDF,再根據A,B,C,D四點共圓的性質,和等腰三角形角之間的關系即可得到.
(2)求△ABC外接圓的面積,只需解出圓半徑,故作等腰三角形底邊上的垂直平分線即過圓心,再連接OC,根據角之間的關系在三角形內即可求得圓半徑,可得到外接圓面積.
點評:此題主要考查圓內接多邊形的性質、圓周角定理、等腰三角形的性質以及三角形的外接圓的性質.此題難度適中,注意掌握輔助線的作法,注意數形結合思想與方程思想的應用.

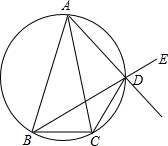 如圖,已知在△ABC中,AB=AC,D是△ABC外接圓劣弧AC上的點(不與A,C重合),延長BD至E.
如圖,已知在△ABC中,AB=AC,D是△ABC外接圓劣弧AC上的點(不與A,C重合),延長BD至E.
 =
= ,
, ∠BAC=
∠BAC= ×30°=15°,
×30°=15°, r,
r, r=1,
r=1, ),
), ).
).
