
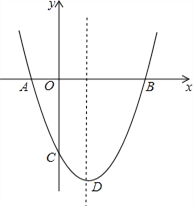
【題目】如圖,拋物線![]() 與y軸交于點
與y軸交于點![]() ,對稱軸為直線
,對稱軸為直線![]() ,點D為拋物線的頂點.
,點D為拋物線的頂點.
![]() 求拋物線解析式和頂點D的坐標;
求拋物線解析式和頂點D的坐標;
![]() 求拋物線與x軸的兩交點A、B的坐標;
求拋物線與x軸的兩交點A、B的坐標;
![]() 你可以直接寫出不等式
你可以直接寫出不等式![]() 的解集嗎?
的解集嗎?
【答案】(1)頂點D的坐標為![]() ;(2)
;(2)![]() 、B的坐標分別為
、B的坐標分別為![]() 、
、![]() ;(3)
;(3)![]() .
.
【解析】試題分析:
(1)把點C(0,-3)代入解析式可得c=-3,由對稱軸為直線x=![]() 可解得b=-2,由此即可得到拋物線的解析式;再把所得解析式配方化為“頂點式”,即可得到頂點坐標;
可解得b=-2,由此即可得到拋物線的解析式;再把所得解析式配方化為“頂點式”,即可得到頂點坐標;
(2)由二次函數解析式中y=0,解得對應的x的值,即可求得A、B兩點的坐標;
(3)由(2)中所求A、B的坐標結合拋物線開口向上即可得到不等式![]() 的解集.
的解集.
試題解析:
(1)∵拋物線![]() 與y軸交于點
與y軸交于點![]() ,對稱軸為直線
,對稱軸為直線![]() ,
,
∴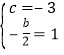 ,解得:b=-2,c=3,
,解得:b=-2,c=3,
∴拋物線的解析式為:y=x2-2x-3,
∵y=x2-2x+3=(x-1)2-4,
∴拋物線的頂點坐標為(1,-4);
(2)在y=x2-2x-3中,當y=0時,x2-2x-3=0,解得:x1=3,x2=-1,
∴A的坐標為(-1,0),B的坐標為(3,0);
(3)∵A的坐標為(-1,0),B的坐標為(3,0),拋物線y=x2-2x-3開口向上,
∴![]() 的解集為:
的解集為:![]() .
.


科目:初中數學 來源: 題型:
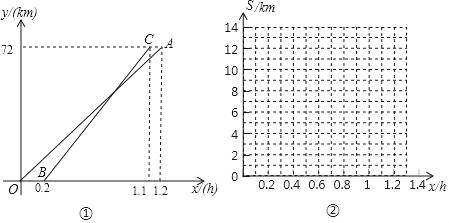
【題目】甲、乙兩人周末從同一地點出發去某景點,因乙臨時有事,甲坐地鐵先出發,甲出發0.2小時后乙開汽車前往.設甲行駛的時間為x(h),甲、乙兩人行駛的路程分別為y1(km)與y2(km).如圖①是y1與y2關于x的函數圖象.
(1)分別求線段OA與線段BC所表示的y1與y2關于x的函數表達式;
(2)當x為多少時,兩人相距6km?
(3)設兩人相距S千米,在圖②所給的直角坐標系中畫出S關于x的函數圖象.
查看答案和解析>>
科目:初中數學 來源: 題型:
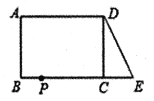
【題目】已知:如圖,在長方形![]() 中,
中,![]() ,
,![]() .延長
.延長![]() 到點
到點![]() ,使
,使![]() ,連接
,連接![]() ,動點
,動點![]() 從點
從點![]() 出發,以每秒2個單位的速度沿
出發,以每秒2個單位的速度沿![]() 向終點
向終點![]() 運動,設點
運動,設點![]() 的運動時間為
的運動時間為![]() 秒,當
秒,當![]() 的值為___________時,
的值為___________時,![]() 和
和![]() 全等.
全等.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一拱橋所在弧所對的圓心角為120°(即∠AOB=120°),半徑為5 m,一艘6 m寬的船裝載一集裝箱,已知箱頂寬3.2 m,離水面AB高2 m,問此船能過橋洞嗎?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
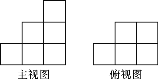
【題目】由一些大小相同的小正方體組成的簡單幾何體的主視圖和俯視圖如圖29-29所示.
(1)請你畫出這個幾何體的一種左視圖.
(2)若組成這個幾何體的小正方體的塊數為n,請你寫出n的所有可能值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 與x軸交于兩點A、
與x軸交于兩點A、![]() 點A在x軸的正半軸上,點B在x軸的負半軸上
點A在x軸的正半軸上,點B在x軸的負半軸上![]() 與y軸交于點C.
與y軸交于點C.
![]() 求m的取值范圍;
求m的取值范圍;
![]() 如果
如果![]() :
:![]() :1,在該拋物線對稱軸右邊圖象上求一點P的坐標,使得
:1,在該拋物線對稱軸右邊圖象上求一點P的坐標,使得![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料后解決問題:
小明遇到下面一個問題:
計算(2+1)(22+1)(24+1)(28+1).
經過觀察,小明發現如果將原式進行適當的變形后可以出現特殊的結構,進而可以應用平方差公式解決問題,具體解法如下:(2+1)(22+1)(24+1)(28+1)
=(2+1)(2﹣1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(28﹣1)(28+1)
=216﹣1
請你根據小明解決問題的方法,試著解決以下的問題:
(1)(2+1)(22+1)(24+1)(28+1)(216+1)=_____.
(2)(3+1)(32+1)(34+1)(38+1)(316+1)=_____.
(3)化簡:(m+n)(m2+n2)(m4+n4)(m8+n8)(m16+n16).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:平面內的直線l1與l2相交于點O,對于該平面內任意一點M,點M到直線l1、l2的距離分別為a、b,則稱有序非負實數對(a,b)是點M的“距離坐標”,根據上述定義,距離坐標為(2,1)的點的個數有( )
A. 2個B. 3個C. 4個D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
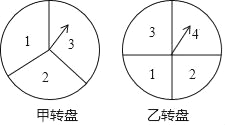
【題目】如圖,甲分為三等分數字轉盤,乙為四等分數字轉盤,自由轉動轉盤.
(1)轉動甲轉盤,指針指向的數字小于3的概率是 ;
(2)同時自由轉動兩個轉盤,用列舉的方法求兩個轉盤指針指向的數字均為奇數的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com