
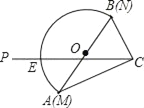
【題目】如圖是一塊含30°(即∠CAB=30°)角的三角板和一個量角器拼在一起,三角板斜邊AB與量角器所在圓的直徑MN重合,其量角器最外緣的讀數是從N點開始(即N點的讀數為0),現有射線CP繞著點C從CA順時針以每秒2度的速度旋轉到與△ACB外接圓相切為止.在旋轉過程中,射線CP與量角器的半圓弧交于E.
(1)當射線CP與△ABC的外接圓相切時,求射線CP旋轉度數是多少?
(2)當射線CP分別經過△ABC的外心、內心時,點E處的讀數分別是多少?
(3)當旋轉7.5秒時,連接BE,求證:BE=CE.
【答案】(1)射線CP旋轉度數是120°;(2)E處的讀數為90;(3)證明見解析.
【解析】
(1) 連接OC. 根據切線的性質, 得∠OCP=![]() , 根據等腰三角形的性質,得∠ACO=∠A, 從而求得射線CP旋轉度數;
, 根據等腰三角形的性質,得∠ACO=∠A, 從而求得射線CP旋轉度數;
(2) 當CP過△ABC外心時 (即過O點)時,∠BCE=![]() , 根據圓周角定理, 則點E處的讀數是
, 根據圓周角定理, 則點E處的讀數是![]() ;當CP過△ABC的內心時, 即CP平分∠ACB, 則∠BCE=
;當CP過△ABC的內心時, 即CP平分∠ACB, 則∠BCE=![]() , 根據圓周角定理,則點E處的讀數是
, 根據圓周角定理,則點E處的讀數是![]() .
.
(3) 根據已知, 知旋轉了![]() , 即可求得∠EBC=∠BCE=
, 即可求得∠EBC=∠BCE=![]() , 從而證明結論.
, 從而證明結論.
(1)連接OC.
∵射線CP與△ABC的外接圓相切,
∴∠OCP=90°,
∵OA=OC,
∴∠ACO=∠A=30°,
∴射線CP旋轉度數是120°;
(2) 
∵∠BCA=90°,
∴△ABC的外接圓就是量角器所在的圓.
當CP過△ABC外心時(即過O點),∠BCE=60°,
∴∠BOE=120°,即E處的讀數為120,
當CP過△ABC的內心時,∠BCE=45°,∠EOB=90°,
∴E處的讀數為90.
(3)在圖2中,
∵∠PCA=2×7.5°=15°,∠BCE=75°,∠ECA=∠EBA=15°,
∴∠EBC=∠EBA+∠ABC=∠BCE=75°,
∴BE=EC.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,已知點P0的坐標為(2,0),將點P0繞著原點O按逆時針方向旋轉60°得點P1,延長OP1到點P2,使OP2=2OP1,再將點P2繞著原點O按逆時針方向旋轉60°得點P3,則點P3的坐標是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
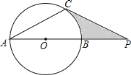
【題目】如圖,已知:![]() 的直徑
的直徑![]() 與弦
與弦![]() 的夾角
的夾角![]() ,過點
,過點![]() 作
作![]() 的切線交
的切線交![]() 的延長線于點
的延長線于點![]() .
.
![]() 求證:
求證:![]() ;
;
![]() 的直徑是
的直徑是![]() ,以點
,以點![]() 為圓心作圓,當半徑為多長時,
為圓心作圓,當半徑為多長時,![]() 與
與![]() 相切?
相切?
![]() 若
若![]() ,求圖中陰影部分的面積(結果精確到
,求圖中陰影部分的面積(結果精確到![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年,長沙開始推廣垃圾分類,分類垃圾桶成為我們生活中的必備工具.某學校開學初購進![]() 型和
型和![]() 型兩種分類垃圾桶,購買
型兩種分類垃圾桶,購買![]() 型垃圾桶花費了2500元,購買
型垃圾桶花費了2500元,購買![]() 型垃圾桶花費了2000元,且購買
型垃圾桶花費了2000元,且購買![]() 型垃圾桶數量是購買
型垃圾桶數量是購買![]() 型垃圾桶數量的2倍,已知購買一個
型垃圾桶數量的2倍,已知購買一個![]() 型垃圾桶比購買一個
型垃圾桶比購買一個![]() 型垃圾桶多花30元.
型垃圾桶多花30元.
(1)求購買一個![]() 型垃圾桶、B型垃圾桶各需多少元?
型垃圾桶、B型垃圾桶各需多少元?
(2)由于實際需要,學校決定再次購買分類垃圾桶,已知此次購進![]() 型和
型和![]() 型兩種分類垃圾桶的數量一共為50個,恰逢市場對這兩種垃圾桶的售價進行調整,
型兩種分類垃圾桶的數量一共為50個,恰逢市場對這兩種垃圾桶的售價進行調整,![]() 型垃圾桶售價比第一次購買時提高了8%,
型垃圾桶售價比第一次購買時提高了8%,![]() 型垃圾桶按第一次購買時售價的9折出售,如果此次購買
型垃圾桶按第一次購買時售價的9折出售,如果此次購買![]() 型和
型和![]() 型這兩種垃圾桶的總費用不超過3240元,那么此次最多可購買多少個
型這兩種垃圾桶的總費用不超過3240元,那么此次最多可購買多少個![]() 型垃圾桶?
型垃圾桶?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角三角形ABC中,∠ACB=90°,∠B=60°,AD,CE是角平分線,AD與CE相交于點F,FM⊥AB,FN⊥BC,垂足分別為M,N.求證:FE=FD.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,點
,點![]() 為
為![]() 的中點.
的中點.
(1)如圖1,E為線段DC上任意一點,將線段![]() 繞點D逆時針旋轉90°得到線段
繞點D逆時針旋轉90°得到線段![]() ,連接
,連接![]() ,過點F作
,過點F作![]() ,交直線
,交直線![]() 于點
于點![]() .判斷
.判斷![]() 與
與![]() 的數量關系并加以證明;
的數量關系并加以證明;
(2)如圖2,若![]() 為線段
為線段![]() 的延長線上任意一點,(1)中的其他條件不變,你在(1)中得出的結論是否發生改變,直接寫出你的結論,不必證明.
的延長線上任意一點,(1)中的其他條件不變,你在(1)中得出的結論是否發生改變,直接寫出你的結論,不必證明.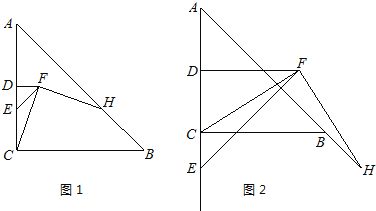
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地計劃用120~180天(含120與180天)的時間建設一項水利工程,工程需要運送的土石方總量為360萬米![]()
(1)設平均每天的工作量為x(單位:萬米![]() ),用
),用![]() 來表示運輸公司完成任務所需的時間,并寫出x的取值范圍.
來表示運輸公司完成任務所需的時間,并寫出x的取值范圍.
(2)由于工程進度的需要,實際平均每天運送土石方是原計劃的1.2倍,工期比原計劃減少了24天,原計劃和實際平均每天運送土石方各是多少米![]() ?
?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com