
【題目】如圖,△ABC中,∠B=∠C=65°,BD=CE,BE=CF,若∠A=50°,則∠DEF的度數是( )

A. ![]()
B. ![]()
C. ![]()
D. ![]()
科目:初中數學 來源: 題型:
【題目】問題背景
在△ABC中,AB,BC,AC的長分別為![]() ,
,![]() ,
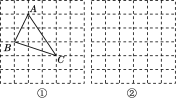
,![]() ,求這個三角形的面積.曉輝同學在解答這道題時,先建立一個正方形網格(每個小正方形的邊長為1),再在網格中畫出格點三角形ABC(即△ABC的三個頂點都在小正方形的頂點處),如圖①所示,這樣不需求△ABC的高,而借用網格就能計算出它的面積.
,求這個三角形的面積.曉輝同學在解答這道題時,先建立一個正方形網格(每個小正方形的邊長為1),再在網格中畫出格點三角形ABC(即△ABC的三個頂點都在小正方形的頂點處),如圖①所示,這樣不需求△ABC的高,而借用網格就能計算出它的面積.
(1)請你直接寫出△ABC的面積:________.
(2)我們把上述求△ABC面積的方法叫做構圖法.若△ABC的三邊長分別為![]() a,2
a,2![]() a,
a,![]() a(a>0),請利用圖②的正方形網格(每個小正方形的邊長為a)畫出相應的△ABC,并求出它的面積.
a(a>0),請利用圖②的正方形網格(每個小正方形的邊長為a)畫出相應的△ABC,并求出它的面積.
探索創新
(3)若△ABC的三邊長分別為![]() ,
,![]() ,2
,2![]() (m>0,n>0,且m≠n),試運用構圖法(自己重新設計一個符合結構特征的網格)求出這個三角形的面積.
(m>0,n>0,且m≠n),試運用構圖法(自己重新設計一個符合結構特征的網格)求出這個三角形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,D,E分別是邊BC,AC上的點,且BD=EC,∠ADE=∠B.
(1)求證:AD=DE;
(2)若∠ADE=![]() ,求∠ADB的度數(用含x的代數式表示).
,求∠ADB的度數(用含x的代數式表示).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知等邊△ABC和等邊△BPE,點P在BC的延長線上,EC的延長線交AP于M,連BM.
(1)求證:AP=CE;
(2)求∠PME的度數;
(3)求證:BM平分∠AME;
(4)AM,BM,MC之間有怎樣的數量關系,直接寫出,不需證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠C=Rt∠,AC=8cm,BC=6cm,若動點P從點C開始,按C→A→B→C的路徑運動,且速度為每秒2cm,設運動的時間為t秒。

(1)當t為何值時,CP把△ABC的周長分成相等的兩部分。
(2)當t為何值時,CP把△ABC的面積分成相等的兩部分,并求出此時CP的長;
(3)當t為何值時,△BCP為等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知矩形ABCD中,AB=1,在BC上取一點E , 沿AE將△ABE向上折疊,使B點落在AD上的F點,若四邊形EFDC與矩形ABCD相似,則AD=( ).
A.![]()
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠B=∠C=36°,AB的垂直平分線交BC于點D,交AB于點H,AC的垂直平分線交BC于點E,交AC于點G,連接AD,AE,則下列結論錯誤的是( ) 
A.![]() =
= ![]()
B.AD,AE將∠BAC三等分
C.△ABE≌△ACD
D.S△ADH=S△CEG
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=x2+bx+c與x軸交于點A、B,AB=2,與y軸交于點C,對稱軸為直線x=2,對稱軸交x軸于點M.
(1)求拋物線的函數解析式;
(2)設P為對稱軸上一動點,求△APC周長的最小值;
(3)設D為拋物線上一點,E為對稱軸上一點,若以點A、B、D、E為頂點的四邊形是菱形,則點D的坐標為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com