
如圖,已知⊙O是正方形ABCD的外接圓,點E是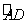 上任意一點,則∠BEC 的度數為 ( )
上任意一點,則∠BEC 的度數為 ( )
A. 30° B. 45° C. 60° D. 90°
 |
 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案科目:初中數學 來源: 題型:
如圖,拋物線y=ax2+bx+c交x軸于點A(-3,0),點B(1,0),交y軸于點E(0,-3).點C是點A關于點B的對稱點,點F是線段BC的中點,直線l過點F且與y軸平行.直線y=-x+m過點C,交y軸于點D.
(1)求拋物線的解析式;
(2)點K為線段AB上一動點,過點K作x軸的垂線,交直線CD于點H,交拋物線于點G,求線段HG長度的最大值;
(3)在直線l上取點M,在拋物線上取點N,使以A,C,M,N為頂點的四邊形是平行四邊形,求點N的坐標.
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
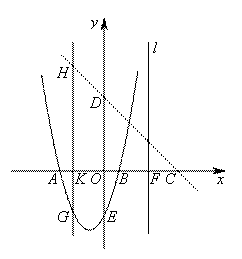
如圖,Rt△ABC的直角邊BC在x軸正半軸上,點D為斜邊AC的中點,DB的延長線交y軸負半軸于點E,反比例函數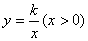 的圖象經過點A.若S△BEC=4,則k的值
的圖象經過點A.若S△BEC=4,則k的值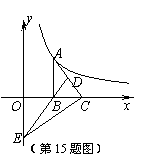 為 ;
為 ;
查看答案和解析>>
科目:初中數學 來源: 題型:
閱讀理解:配方法是中學數學的重要方法,用配方法可求最大(小)值。
對于任意正實數a、b,可作如下變形a+b=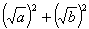 =
=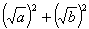 -
- +
+ =
= +
+  ,
,
又∵ ≥0, ∴
≥0, ∴ +
+  ≥0+
≥0+ ,即
,即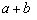 ≥
≥ .
.
(1)根據上述內容,回答下列問題:在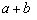 ≥
≥ (a、b均為正實數)中,若ab為定值p,則a+b≥
(a、b均為正實數)中,若ab為定值p,則a+b≥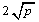 ,當且僅當a、b滿足 時,a+b有最小值
,當且僅當a、b滿足 時,a+b有最小值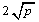 .
.
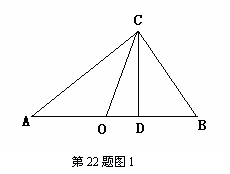
(2)思考驗證:如圖1,△ABC中,∠ACB=90°,CD⊥AB,垂足為D,CO為AB邊上中線,AD=2a,DB=2b, 試根據圖形驗證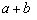 ≥
≥ 成立,并指出等號成立時的條件.
成立,并指出等號成立時的條件.
 (3)探索應用:如圖2,已知A為反比例函數
(3)探索應用:如圖2,已知A為反比例函數 的圖像上一點,A點的橫坐標為1,將一塊三角板的直角頂點放在A處旋轉,保持兩直角邊始終與x軸交于兩點D、E,F(0,-3)為y軸上一點,連結DF、EF,求四邊形ADFE面積的最小值.
的圖像上一點,A點的橫坐標為1,將一塊三角板的直角頂點放在A處旋轉,保持兩直角邊始終與x軸交于兩點D、E,F(0,-3)為y軸上一點,連結DF、EF,求四邊形ADFE面積的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
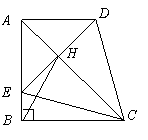
在直角梯形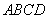 中,
中, ,
,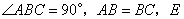 為
為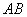 邊上一點,
邊上一點, ,且
,且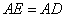 .連接
.連接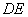 交對角線
交對角線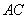 于
于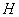 ,連接
,連接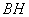 .下列結論:
.下列結論:
①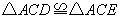 ;②
;②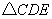 為等邊三角形;③
為等邊三角形;③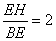 ; ④.
; ④.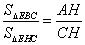
其中結論正確的是( )
A.只有①② B.只有①②④ C.只有③④ D.①②③④
 |
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,A、M是反比例函數 的圖象上的兩點,過點M作直線MB∥x軸,交
的圖象上的兩點,過點M作直線MB∥x軸,交 軸于點B;過點
軸于點B;過點 作直線
作直線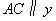 軸交
軸交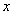 軸于點
軸于點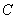 ,交直線MB于點D.BM:DM=8:9,當四邊形OADM的面積為
,交直線MB于點D.BM:DM=8:9,當四邊形OADM的面積為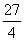 時,k= .
時,k= .
查看答案和解析>>
科目:初中數學 來源: 題型:
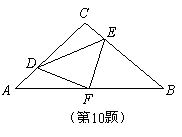
如圖,在等腰 中,
中,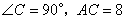 ,F是AB邊上的中點,點D、E分別在AC、BC邊上運動,且保持
,F是AB邊上的中點,點D、E分別在AC、BC邊上運動,且保持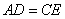 .連接DE、DF、EF.在此運動變化的過程中,下列結論:①
.連接DE、DF、EF.在此運動變化的過程中,下列結論:①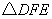 是等腰直角三角形;②四邊形CDFE不可能為正方形,③DE長度的最小值為4;④四邊形CDFE的面積保持不變;⑤△CDE面積的最大值為8.其中正確的結論是( )
是等腰直角三角形;②四邊形CDFE不可能為正方形,③DE長度的最小值為4;④四邊形CDFE的面積保持不變;⑤△CDE面積的最大值為8.其中正確的結論是( )
A.①④⑤ B.③④⑤ C.①③④ D.①②③


查看答案和解析>>
科目:初中數學 來源: 題型:
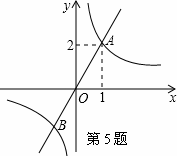
如圖,函數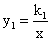 與
與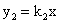 的圖象相交于點A(1,2)和點B,當y1>y2時的變量x的取值范圍是( )(原創)
的圖象相交于點A(1,2)和點B,當y1>y2時的變量x的取值范圍是( )(原創)
A、x>1 B、-1<x<0 C、-1<x<0或x>1 D、x<-1或0<x<1
 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com