
【題目】如圖,已知拋物線y=![]() +mx+3與x軸交于A,B兩點,與y軸交于點C,點B的坐標為(3,0),
+mx+3與x軸交于A,B兩點,與y軸交于點C,點B的坐標為(3,0),
(1)求m的值及拋物線的頂點坐標.
(2)點P是拋物線對稱軸l上的一個動點,當PA+PC的值最小時,求點P的坐標.

【答案】(1)m=2,(1,4);(2)(1,2).
【解析】試題分析:(1)首先把點B的坐標為(3,0)代入拋物線y=![]() +mx+3,利用待定系數法即可求得m的值,繼而求得拋物線的頂點坐標;
+mx+3,利用待定系數法即可求得m的值,繼而求得拋物線的頂點坐標;
(2)首先連接BC交拋物線對稱軸l于點P,則此時PA+PC的值最小,然后利用待定系數法求得直線BC的解析式,繼而求得答案.
試題解析:(1)把點B的坐標為(3,0)代入拋物線y=![]() +mx+3得:0=
+mx+3得:0=![]() +3m+3,
+3m+3,
解得:m=2,
∴y=![]() +2x+3=
+2x+3=![]() ,
,
∴頂點坐標為:(1,4).
(2)連接BC交拋物線對稱軸l于點P,則此時PA+PC的值最小,
設直線BC的解析式為:y=kx+b,
∵點C(0,3),點B(3,0),
∴![]() ,解得:
,解得: ![]() ,
,
∴直線BC的解析式為:y=﹣x+3,
當x=1時,y=﹣1+3=2,
∴當PA+PC的值最小時,點P的坐標為:(1,2).



 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:初中數學 來源: 題型:
【題目】下列語句:
①對頂角相等
②如果兩條平行線被第三條截,同旁內角相等,那么這兩條平行線都與第三條直線垂直;
③過一點有且只有一條直線與已知直線平行,其中( )
A.①、②是正確的命題B.②、③是正確命題
C.①、③是正確命題D.以上結論皆錯
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中:全等三角形的對應邊相等;全等三角形的對應角相等;全等三角形的周長相等;周長相等的兩個三角形全等;全等三角形的面積相等;面積相等的兩個三角形全等,正確說法有( )
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點E,C在線段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.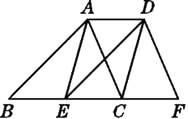
(1)求證:△ABC≌△DEF;
(2)試判斷:四邊形AECD的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=AC,點D在邊BC所在的直線上,過點D作DE∥AC交直線AB于點E,DF∥AB交直線AC于點F.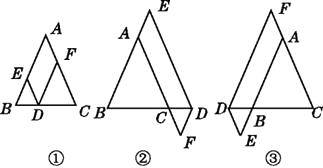
(1)當點D在邊BC上時,如圖①,求證:DE+DF=AC.
(2)當點D在邊BC的延長線上時,如圖②;當點D在邊BC的反向延長線上時,如圖③.請分別寫出圖②、圖③中DE,DF,AC之間的數量關系,不需要證明.
(3)若AC=6,DE=4,則DF=.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com