
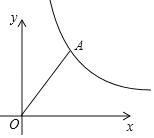
【題目】如圖,已知反比例函數y=![]() (x>0)的圖象經過點A(3,4),在該圖象上找一點B,使tan∠BOA=
(x>0)的圖象經過點A(3,4),在該圖象上找一點B,使tan∠BOA=![]() ,則點B的坐標為_____.
,則點B的坐標為_____.
【答案】(2![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
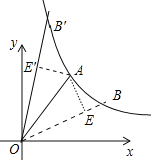
如圖取點E(4,2),連接AE,OE.證明△ABE是直角三角形,tan∠BOA=![]() ,求出直線OE與反比例函數的圖象的交點即可解決問題,再根據軸對稱性可求出符合題意的另一點E’.
,求出直線OE與反比例函數的圖象的交點即可解決問題,再根據軸對稱性可求出符合題意的另一點E’.
如圖取點E(4,2),連接AE,OE.
∵A(3,4),
∴OA=![]() =5,AE=
=5,AE=![]() =
=![]() ,OE=
,OE=![]() =2
=2![]() ,
,
∴OA2=AE2+OE2=25,
∴∠AEO=90°,
∴tan∠AOE=![]() =
=![]() ,
,
延長OE交反比例函數的圖象于B,點B即為所求,
∵A(3,4)在y=![]() 上,
上,
∴k=12,
∵直線OE的解析式為y=![]() x,
x,
由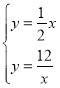 ,解得
,解得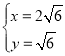 或
或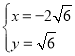 (舍棄),
(舍棄),
∴B(2![]() ,
,![]() ),
),
作點E關于直線OA的對稱點E′,則E′(![]() ,
,![]() ),射線OE′交反比例函數的圖象于B′,則點B′即為所求,
),射線OE′交反比例函數的圖象于B′,則點B′即為所求,
∴直線OE′的解析式為y=![]() x,
x,
由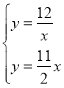 ,解得
,解得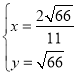 或
或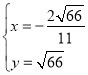 (舍棄),
(舍棄),
∴B′(![]() ,
,![]() ),
),
綜上所述,滿足條件的點B的坐標為(2![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
故答案為(2![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【點晴】
本題考查反比例函數圖象上點的坐標特征,一次函數的應用等知識,解題的關鍵是學會尋找特殊點解決問題,學會構建一次函數,利用方程組確定交點坐標是解題的關鍵.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:初中數學 來源: 題型:
【題目】美麗的黃河宛如一條玉帶穿城而過,沿河兩岸的濱河路風情線是蘭州最美的景觀之一.數學課外實踐活動中,小林在南濱河路上的A,B兩點處,利用測角儀分別對北岸的一觀景亭D進行了測量.如圖,測得∠DAC=45°,∠DBC=65°.若AB=132米,求觀景亭D到南濱河路AC的距離(結果精確到1米,參考數據:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于x的方程![]() 有兩個不相等的實數根.
有兩個不相等的實數根.
(1)求m的取值范圍;
(2)是否存在實數m,使方程的兩個實數根的倒數和等于0?若存在,求出m的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
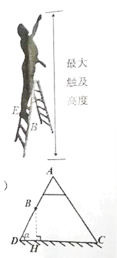
【題目】某電工想換房間的燈泡,已知燈泡到地面的距離為![]() ,現有一架家用可調節式腳踏人字梯,其中踏板、地面都是水平的.梯子的側面簡化結構如圖所示,左右支撐架長度相等,
,現有一架家用可調節式腳踏人字梯,其中踏板、地面都是水平的.梯子的側面簡化結構如圖所示,左右支撐架長度相等,![]() .設梯子一邊
.設梯子一邊![]() 與地面的夾角為
與地面的夾角為![]() ,且
,且![]() 可調節的范圍為
可調節的范圍為![]() .當
.當![]() 時,電工站在梯子安全擋中最高一檔踏板
時,電工站在梯子安全擋中最高一檔踏板![]() 上的最大觸及高度為
上的最大觸及高度為![]() .
.
(1)當![]() 時,求踏板
時,求踏板![]() 離地面的高度
離地面的高度![]() .(精確到
.(精確到![]() )
)
(2)調節角度,試判斷電工是否可以換下燈泡,并說明理由.(參考數據:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
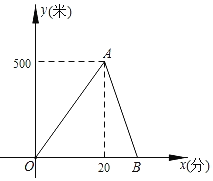
【題目】某湖邊健身步道全長1500米,甲、乙兩人同時從同一起點勻速向終點步行.甲先到達終點后立刻返回,在整個步行過程中,甲、乙兩人間的距離y(米)與出發的時間x(分)之間的關系如圖中OA﹣AB折線所示.
(1)用文字語言描述點A的實際意義;
(2)求甲、乙兩人的速度及兩人相遇時x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
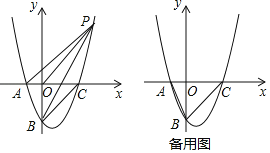
【題目】已知拋物線y=![]() x2+bx+c經過點A(﹣2,0),B(0、﹣4)與x軸交于另一點C,連接BC.
x2+bx+c經過點A(﹣2,0),B(0、﹣4)與x軸交于另一點C,連接BC.
(1)求拋物線的解析式;
(2)如圖,P是第一象限內拋物線上一點,且S△PBO=S△PBC,求證:AP∥BC;
(3)在拋物線上是否存在點D,直線BD交x軸于點E,使△ABE與以A,B,C,E中的三點為頂點的三角形相似(不重合)?若存在,請求出點D的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,點E是AD上的一個動點,連接BE,作點A關于BE的對稱點F,且點F落在矩形ABCD的內部,連接AF,BF,EF,過點F作GF⊥AF交AD于點G,設![]() .
.
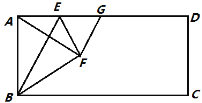
(1)求證:AE=GE;
(2)當點F落在AC上時,用含n的代數式表示![]() 的值;
的值;
(3)若AD=4AB,且以點F,C,G為頂點的三角形是直角三角形,求n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
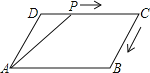
【題目】如圖,在平行四邊形ABCD中,∠DAB=60°,AB=5,BC=3,點P從點D出發,沿DC,CB向終點B勻速運動.設點P所走過的路程為x,點P所經過的線段與AD,AP所圍成的圖形的面積為y,y隨x的變化而變化.在下列圖象中,能正確反映y與x的函數關系的是( )
A.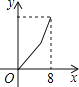 B.
B. C.
C.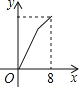 D.
D.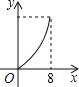
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有A、B兩組卡片共5張,A組的三張分別寫有數字2,4,6,B組的兩張分別寫有3,5.它們除了數字外沒有任何區別,
(1)隨機從A組抽取一張,求抽到數字為2的概率;
(2)隨機地分別從A組、B組各抽取一張,請你用列表或畫樹狀圖的方法表示所有等可能的結果.現制定這樣一個游戲規則:若選出的兩數之積為3的倍數,則甲獲勝;否則乙獲勝.請問這樣的游戲規則對甲乙雙方公平嗎?為什么?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com