
如圖,在平面直角坐標系中,直線 與拋物線
與拋物線 交于A、B兩點,點A在x軸上,點B的橫坐標為-8.
交于A、B兩點,點A在x軸上,點B的橫坐標為-8.
(1)求該拋物線的解析式;
(2)點P是直線AB上方的拋物線上一動點(不與點A、B重合),過點P作x軸的垂線,垂足為C,交直線AB于點D,作PE⊥AB于點E.
①設△PDE的周長為l,點P的橫坐標為x,求l關于x的函數關系式,并求出l的最大值;
②連接PA,以PA為邊作圖示一側的正方形APFG.隨著點P的運動,正方形的大小、位置也隨之改變.當頂點F或G恰好落在y軸上時,直接寫出對應的點P的坐標.
(1)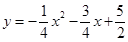 ;
;
(2)①x=﹣3時,l最大=15;
②點P有三個,分別是P1(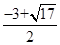 ,2),P2(
,2),P2( ,2),P3(
,2),P3(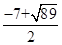 ,
,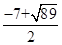 ).
).
解析試題分析:(1)利用待定系數法求出b,c即可;
(2)①根據△AOM∽△PED,得出DE:PE:PD=3:4:5,再求出PD=yP﹣yD求出二函數最值即可;
②當點G落在y軸上時,由△ACP≌△GOA得PC=AO=2,即 ,解得
,解得 ,
,
所以得出P點坐標,當點F落在y軸上時,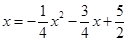 ,解得
,解得 ,可得P點坐標.
,可得P點坐標.
試題解析:(1)對于 ,當y=0,x=2.當x=﹣8時,y=﹣
,當y=0,x=2.當x=﹣8時,y=﹣ .
.
∴A點坐標為(2,0),B點坐標為(﹣8,﹣ ).
).
由拋物線 經過A、B兩點,
經過A、B兩點,
得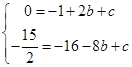
解得 .
.
∴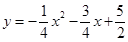 ;
;
(2)①設直線 與y軸交于點M,
與y軸交于點M,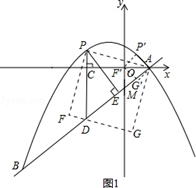
當x=0時,y= .∴OM=
.∴OM= .
.
∵點A的坐標為(2,0),∴OA=2.∴AM=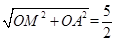 .
.
∵OM:OA:AM=3:4:5.
由題意得,∠PDE=∠OMA,∠AOM=∠PED=90°,∴△AOM∽△PED.
∴DE:PE:PD=3:4:5.
∵點P是直線AB上方的拋物線上一動點,
∵PD⊥x軸,
∴PD兩點橫坐標相同,
∴PD=yP﹣yD=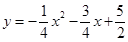 ﹣(
﹣(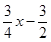 )=﹣
)=﹣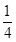 x2﹣
x2﹣ x+4,
x+4,
∴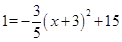 .
.
∴x=﹣3時,l最大=15;
②當點G落在y軸上時,如圖2,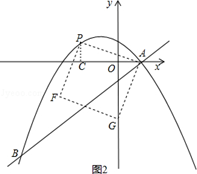
由△ACP≌△GOA得PC=AO=2,
即 ,解得
,解得 ,
,
所以P1(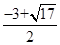 ,2),P2(
,2),P2( ,2),
,2),
如圖3,過點P作PN⊥y軸于點N,過點P作PS⊥x軸于點S,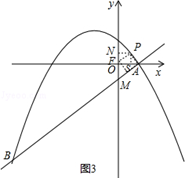
由△PNF≌△PSA,
PN=PS,可得P點橫縱坐標相等,
故得當點F落在y軸上時,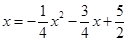 ,解得
,解得 ,
,
可得P3(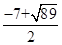 ,
,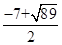 ),P4(
),P4(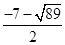 ,
,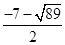 ),(舍去).
),(舍去).
綜上所述:滿足題意的點P有三個,分別是P1(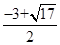 ,2),P2(
,2),P2( ,2),P3(
,2),P3(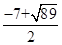 ,
,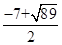 ).
).
考點:二次函數綜合題.


科目:初中數學 來源: 題型:解答題
如圖1,在平面直角坐標系xOy中,點M為拋物線 的頂點,過點(0,4)作x軸的平行線,交拋物線于點P、Q(點P在Q的左側),PQ=4.
的頂點,過點(0,4)作x軸的平行線,交拋物線于點P、Q(點P在Q的左側),PQ=4.
(1)求拋物線的函數關系式,并寫出點P的坐標;
(2)小麗發現:將拋物線 繞著點P旋轉180°,所得新拋物線的頂點恰為坐標原點O,你認為正確嗎?請說明理由;
繞著點P旋轉180°,所得新拋物線的頂點恰為坐標原點O,你認為正確嗎?請說明理由;
(3)如圖2,已知點A(1,0),以PA為邊作矩形PABC(點P、A、B、C按順時針的方向排列), .
.
①寫出C點的坐標:C( , )(坐標用含有t的代數式表示);
②若點C在題(2)中旋轉后的新拋物線上,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,拋物線y=﹣x2+3x+4與x軸交于A、B兩點,與y軸交于C點,點D在拋物線上且橫坐標為3.
(1)求tan∠DBC的值;
(2)點P為拋物線上一點,且∠DBP=45°,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
定義1:在△ABC中,若頂點A,B,C按逆時針方向排列,則規定它的面積為“有向面積”;若頂點A,B,C按順時針方向排列,則規定它的面積的相反數為△ABC的“有向面積”.“有向面積”用 表示,例如圖1中,
表示,例如圖1中, ,圖2中,
,圖2中, .
.
定義2:在平面內任取一個△ABC和點P(點P不在△ABC的三邊所在直線上),稱有序數組( ,
, ,
, )為點P關于△ABC的“面積坐標”,記作
)為點P關于△ABC的“面積坐標”,記作 ,例如圖3中,菱形ABCD的邊長為2,
,例如圖3中,菱形ABCD的邊長為2, ,則
,則 ,點G關于△ABC的“面積坐標”
,點G關于△ABC的“面積坐標” 為
為 .在圖3中,我們知道
.在圖3中,我們知道 ,利用“有向面積”,我們也可以把上式表示為:
,利用“有向面積”,我們也可以把上式表示為: .
.
應用新知:
(1)如圖4,正方形ABCD的邊長為1,則 ,點D關于△ABC的“面積坐標”是 ;探究發現:
,點D關于△ABC的“面積坐標”是 ;探究發現:
(2)在平面直角坐標系 中,點
中,點 ,
,
①若點P是第二象限內任意一點(不在直線AB上),設點P關于 的“面積坐標”為
的“面積坐標”為 ,
,
試探究 與
與 之間有怎樣的數量關系,并說明理由;
之間有怎樣的數量關系,并說明理由;
②若點 是第四象限內任意一點,請直接寫出點P關于
是第四象限內任意一點,請直接寫出點P關于 的“面積坐標”(用x,y表示);
的“面積坐標”(用x,y表示);
解決問題:
(3)在(2)的條件下,點 ,點Q在拋物線
,點Q在拋物線 上,求當
上,求當 的值最小時,點Q的橫坐標.
的值最小時,點Q的橫坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,直線y= x+m與拋物線y=
x+m與拋物線y= x2-2x+l交于不同的兩點M、N(點M在點N的左側).
x2-2x+l交于不同的兩點M、N(點M在點N的左側).
(1)設拋物線的頂點為B,對稱軸l與直線y= x+m的交點為C,連結BM、BN,若S△MBC=
x+m的交點為C,連結BM、BN,若S△MBC= S△NBC,求直線MN的解析式;
S△NBC,求直線MN的解析式;
(2)在(1)條件下,已知點P(t,0)為x軸上的一個動點,
①若△PMN為直角三角形,求點P的坐標.
②若∠MPN>90°,則t的取值范圍是 .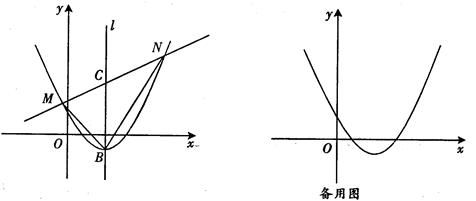
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
拋物線 (b,c均為常數)與x軸交于
(b,c均為常數)與x軸交于 兩點,與y軸交于點
兩點,與y軸交于點 .
.
(1)求該拋物線對應的函數表達式;
(2)若P是拋物線上一點,且點P到拋物線的對稱軸的距離為3,請直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,拋物線y=x²+bx+c與直線y=x-1交于A、B兩點.點A的橫坐標為-3,點B在y軸上,點P是y軸左側拋物線上的一動點,橫坐標為m,過點P作PC⊥x軸于C,交直線AB于D.
(1)求拋物線的解析式;
(2)當m為何值時, ;
;
(3)是否存在點P,使△PAD是直角三角形,若存在,求出點P的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,拋物線 與x軸交于A(5,0)、B(-1,0)兩點,過點A作直線AC⊥x軸,交直線
與x軸交于A(5,0)、B(-1,0)兩點,過點A作直線AC⊥x軸,交直線 于點C;
于點C;
(1)求該拋物線的解析式;
(2)求點A關于直線 的對稱點
的對稱點 的坐標,判定點
的坐標,判定點 是否在拋物線上,并說明理由;
是否在拋物線上,并說明理由;
(3)點P是拋物線上一動點,過點P作y軸的平行線,交線段 于點M,是否存在這樣的點P,使四邊形PACM是平行四邊形?若存在,求出點P的坐標;若不存在,請說明理由.
于點M,是否存在這樣的點P,使四邊形PACM是平行四邊形?若存在,求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
心理學家通過實驗發現:初中學生聽講的注意力隨時間變化,講課開始時,學生注意力逐漸增強,中間有一段平穩狀態,隨后開始分散.學生注意力指標數y隨時間表t(分鐘)變化的函數圖象如下.當0≤t≤10時,圖像是拋物線的一部分,當10≤t≤20時和20≤t≤40時,圖像是線段。
(1)當0≤t≤10時,求注意力指標數y與時間t的函數關系式;
(2)一道數學探究題需要講解24分鐘,問老師能否經過恰當安排,使學生在探究這道題時,注意力指標數不低于45?請通過計算說明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com