
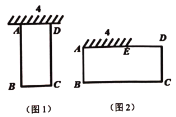
【題目】如圖,校園空地上有一面墻,長度為4米,為了創建“美麗校園”,學校決定借用這面墻和20米的圍欄圍成一個矩形花園![]() ,設
,設![]() 長為
長為![]() 米,矩形花園
米,矩形花園![]() 的面積為
的面積為![]() 平方米.
平方米.
(1)如圖1,若所圍成的矩形花園![]() 邊的長不得超出這面墻,求
邊的長不得超出這面墻,求![]() 關于
關于![]() 的函數關系式,并寫出自變量
的函數關系式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(2)在(1)的條件下,當![]() 為何值時,矩形花園
為何值時,矩形花園![]() 的面積最大,最大值是多少?
的面積最大,最大值是多少?
(3)如圖2,若圍成的矩形花園![]() 的
的![]() 邊的長可超出這面墻,求圍成的矩形
邊的長可超出這面墻,求圍成的矩形![]() 的最大面積.
的最大面積.
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線y=﹣5x+5與x軸、y軸分別交于A,C兩點,拋物線y=x2+bx+c經過A,C兩點,與x軸交于另一點B.
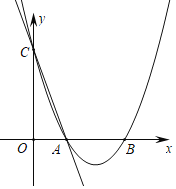
(1)求拋物線解析式及B點坐標;
(2)x2+bx+c≤﹣5x+5的解集是 ;
(3)若點M為拋物線上一動點,連接MA、MB,當點M運動到某一位置時,△ABM面積為△ABC的面積的![]() 倍,求此時點M的坐標.
倍,求此時點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】己知反比例函數![]() (
(![]() 常數,
常數,![]() ).
).
(1)若點![]()
![]() 在這個函數的圖象上,求
在這個函數的圖象上,求![]() 的值;
的值;
(2)若在這個函數圖象的每一個分支上,![]() 隨
隨![]() 的增大而增大,求
的增大而增大,求![]() 的取值范圍;
的取值范圍;
(3)若![]() ,試判斷點
,試判斷點![]()
![]() 是否在這個函數的圖象上,并說明理由.
是否在這個函數的圖象上,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AD是△ABC的中線,tanB=![]() ,cosC=
,cosC=![]() ,AC=
,AC=![]()
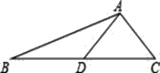
(1)求BC的長;
(2)作出△ABC的外接圓(尺規作圖,保留痕跡,不寫作法),并求外接圓半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解市民對全市創文工作的滿意程度,某中學數學興趣小組在全市甲、乙兩個區內進行了調查統計,將調查結果分為不滿意,一般,滿意,非常滿意四類,回收、整理好全部問卷后,得到下列不完整的統計圖.

請結合圖中信息,解決下列問題:
(1)求此次調查中接受調查的人數.
(2)求此次調查中結果為非常滿意的人數.
(3)興趣小組準備從調查結果為不滿意的4位市民中隨機選擇2位進行回訪,已知4位市民中有2位來自甲區,另2位來自乙區,請用列表或用畫樹狀圖的方法求出選擇的市民均來自甲區的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線![]() 與
與![]() 軸、
軸、![]() 軸分別相交于點A(-1,0)和B(0,3),其頂點為D。
軸分別相交于點A(-1,0)和B(0,3),其頂點為D。
(1)求這條拋物線的解析式;
(2)畫出此拋物線;
(3)若拋物線與![]() 軸的另一個交點為E,求△ODE的面積;
軸的另一個交點為E,求△ODE的面積;
(4)拋物線的對稱軸上是否存在點P使得△PAB的周長最短。若存在請求出點P的坐標,若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在汛期到來之際,某水泵廠接到生產一批小型抽水泵的緊急任務。要求必須在10天內(含10天)完成任務。為提高生產效率,工廠加班加點,接到任務的第一天就生產了水泵20臺,以后每天生產的水泵都比前一天多2 臺。由于機器損耗等原因,當日生產的水泵數量達到28臺后,每多生產一臺,當天生產的所有水泵,平均每臺成本就增加20元。
(1)設第![]() 天生產水泵
天生產水泵![]() 臺,直接寫出
臺,直接寫出![]() 與
與![]() 之間的函數解析式,并寫出自變量
之間的函數解析式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(2)若每臺水泵的成本價(日生產量不超過28臺時)為1000元,銷售價格為每臺1400元,設第![]() 天的利潤為
天的利潤為![]() 元,試求
元,試求![]() 與
與![]() 之間的函數解析式,并求該廠哪一天獲得的利潤最大,最大利潤最多少?
之間的函數解析式,并求該廠哪一天獲得的利潤最大,最大利潤最多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“特色泰興,美好生活”, 泰興舉行金色秋天旅游活動.明明和華華同學分析網上關于旅游活動的信息,發現最具特色的景點有:①小南湖、②古銀杏公園、③紅楓園.他們準備周日下午去參觀游覽,各自在這三中個景點任選一個,每個景點被選中的可能性相同.
(1)明明同學在三個備選景點中選中小南湖的概率是_____.
(2)用樹狀圖或列表法求出明明和華華他們選中不同景點參觀的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:平行四邊形ABCD的兩邊AB、BC的長是關于x的方程x2﹣mx+![]() ﹣
﹣![]() =0的兩個實數根.
=0的兩個實數根.
(1)試說明:無論m取何值方程總有兩個實數根
(2)當m為何值時,四邊形ABCD是菱形?求出這時菱形的邊長;
(3)若AB的長為2,那么平行四邊形ABCD的周長是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com