
【題目】如圖,矩形![]() 中,
中,![]() ,把矩形沿對角線
,把矩形沿對角線![]() 所在直線折疊,使點
所在直線折疊,使點![]() 落在點
落在點![]() 處,
處,![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() .
.
(1)求證:![]() ;
;
(2)求證:![]() 是等腰三角形.
是等腰三角形.
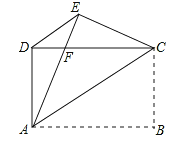
【答案】(1)證明見解析;(2)證明見解析.
【解析】
(1)根據矩形的性質可得出AD=BC,AB=CD,結合折疊的性質可得出AD=CE,AE=CD,進而即可證出△ADE≌△CED(SSS);
(2)根據全等三角形的性質可得出∠DEF=∠EDF,利用等邊對等角可得出EF=DF ,由此即可證出△DEF是等腰三角形.
(1)∵四邊形ABCD是矩形,
∴AD=BC,AB=CD.
由折疊的性質可得:BC=CE,AB=AE,
∴AD=CE,AE=CD.
在△ADE和△CED中,
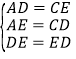 ,
,
∴△ADE≌△CED(SSS).
(2)由(1)得△ADE≌△CED,
∴∠DEA=∠EDC,
即∠DEF=∠EDF,
∴EF=DF,
∴△DEF是等腰三角形.


 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案科目:初中數學 來源: 題型:
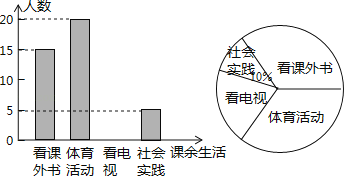
【題目】為了解某中學學生課余生活情況,對喜愛看課外書、體育活動、看電視、社會實踐四個方面的人數進行調查統計.現從該校隨機抽取![]() 名學生作為樣本,采用問卷調查的方法收集數據(參與問卷調查的每名學生只能選擇其中一項).并根據調查得到的數據繪制成了如圖所示的兩幅不完整的統計圖.由圖中提供的信息,解答下列問題:
名學生作為樣本,采用問卷調查的方法收集數據(參與問卷調查的每名學生只能選擇其中一項).并根據調查得到的數據繪制成了如圖所示的兩幅不完整的統計圖.由圖中提供的信息,解答下列問題:
(1)求n的值;
(2)若該校學生共有1200人,試估計該校喜愛看電視的學生人數;
(3)若調查到喜愛體育活動的4名學生中有3名男生和1名女生,現從這4名學生中任意抽取2名學生,求恰好抽到2名男生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
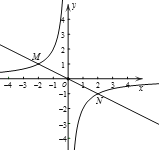
【題目】如圖,反比例函數![]() 的圖象與一次函數
的圖象與一次函數![]() 的圖象分別交于M,N兩點,已知點M(-2,m).
的圖象分別交于M,N兩點,已知點M(-2,m).
(1)求反比例函數的表達式;
(2)點P為y軸上的一點,當∠MPN為直角時,直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把平面內一條數軸x繞原點O逆時針旋轉角θ(0°<θ<90°)得到另一條數軸y,x軸和y軸構成一個平面斜坐標系.規定:過點P作y軸的平行線,交x軸于點A,過點P作x軸的平行線,交y軸于點B,若點A在x軸上對應的實數為a,點B在y軸上對應的實數為b,則稱有序實數對(a,b)為點P的斜坐標,在某平面斜坐標系中,已知θ=60°,點M′的斜坐標為(3,2),點N與點M關于y軸對稱,則點N的斜坐標為_____.
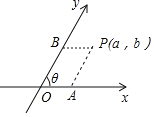
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】空間任意選定一點O,以點O為端點,作三條互相垂直的射線ox、oy、oz.這三條互相垂直的射線分別稱作x軸、y軸、z軸,統稱為坐標軸,它們的方向分別為ox(水平向前)、oy(水平向右)、oz(豎直向上)方向,這樣的坐標系稱為空間直角坐標系.
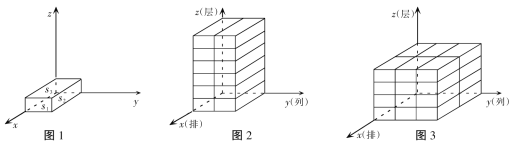
將相鄰三個面的面積記為S1、S2、S3,且S1<S2<S3的小長方體稱為單位長方體,現將若干個單位長方體在空間直角坐標系內進行碼放,要求碼放時將單位長方體S1所在的面與x軸垂直,S2所在的面與y軸垂直,S3所在的面與z軸垂直,如圖1所示.
若將x軸方向表示的量稱為幾何體碼放的排數,y軸方向表示的量稱為幾何體碼放的列數,z軸方向表示的量稱為幾何體碼放的層數;如圖2是由若干個單位長方體在空間直角坐標內碼放的一個幾何體,其中這個幾何體共碼放了1排2列6層,用有序數組記作(1,2,6),如圖3的幾何體碼放了2排3列4層,用有序數組記作(2,3,4).這樣我們就可用每一個有序數組(x,y,z)表示一種幾何體的碼放方式.
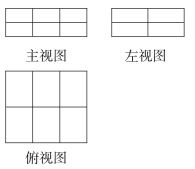
(1)如圖是由若干個單位長方體碼放的一個幾何體的三視圖,寫出這種碼放方式的有序數組,組成這個幾何體的單位長方體的個數為多少個;
(2)對有序數組性質的理解,下列說法正確的是哪些;(只寫序號)
①每一個有序數組(x,y,z)表示一種幾何體的碼放方式.
②有序數組中x、y、z的乘積就表示幾何體中單位長方體的個數.
③有序數組不同,所表示幾何體的單位長方體個數不同.
④不同的有序數組所表示的幾何體的體積不同.
⑤有序數組中x、y、z每兩個乘積的2倍可分別確定幾何體表面上S1、S2、S3的個數.
(3)為了進一步探究有序數組(x,y,z)的幾何體的表面積公式S(x,y,z),某同學針對若干個單位長方體進行碼放,制作了下列表格:
幾何體 有序數組 | 單位長方體的個數 | 表面上面積為 | 表面上面積為 | 表面上面積為 | 表面積 |
(1,1,1) | 1 | 2 | 2 | 2 | 2S1+2S2+2S3 |
(1,2,1) | 2 | 4 | 2 | 4 | 4S1+2S2+4S3 |
(3,1,1) | 3 | 2 | 6 | 6 | 2S1+6S2+6S3 |
(2,1,2) | 4 | 4 | 8 | 4 | 4S1+8S2+4S3 |
(1,5,1) | 5 | 10 | 2 | 10 | 10S1+2S2+10S3 |
(1,2,3) | 6 | 12 | 6 | 4 | 12S1+6S2+4S3 |
(1,1,7) | 7 | 14 | 14 | 2 | 14S1+14S2+2S3 |
(2,2,2) | 8 | 8 | 8 | 8 | 8S1+8S2+8S3 |
… | … | … | … | … | … |
根據以上規律,請寫出有序數組(x,y,z)的幾何體表面積計算公式S(x,y,z);(用x、y、z、S1、S2、S3表示)
(4)當S1=2,S2=3,S3=4時,對由12個單位長方體碼放的幾何體進行打包,為了節約外包裝材料,對12個單位長方體碼放的幾何體表面積最小的規律進行探究,根據探究的結果請寫出使幾何體表面積最小的有序數組,并用幾何體表面積公式求出這個最小面積.(縫隙不計)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系內,以原點O為圓心,1為半徑作圓,點P在直線![]() 上運動,過點P作該圓的一條切線,切點為A,則PA的最小值為
上運動,過點P作該圓的一條切線,切點為A,則PA的最小值為![]()
![]()
A. 3 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小玲和弟弟小東分別從家和圖書館同時出發,沿同一條路相向而行,小玲開始跑步中途改為步行,到達圖書館恰好用30min.小東騎自行車以300m/min的速度直接回家,兩人離家的路程y(m)與各自離開出發地的時間x(min)之間的函數圖象如圖所示
(1)家與圖書館之間的路程為多少m,小玲步行的速度為多少m/min;
(2)求小東離家的路程y關于x的函數解析式,并寫出自變量的取值范圍;
(3)求兩人相遇的時間.

查看答案和解析>>
科目:初中數學 來源: 題型:
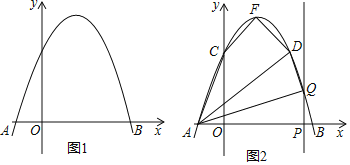
【題目】如圖1,拋物線y=ax2+bx+3交x軸于點A(﹣1,0)和點B(3,0).
(1)求該拋物線所對應的函數解析式;
(2)如圖2,該拋物線與y軸交于點C,頂點為F,點D(2,3)在該拋物線上.
①求四邊形ACFD的面積;
②點P是線段AB上的動點(點P不與點A、B重合),過點P作PQ⊥x軸交該拋物線于點Q,連接AQ、DQ,當△AQD是直角三角形時,求出所有滿足條件的點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O 的直徑,點D在⊙O 上(點D不與A,B重合),直線AD交過點B的切線于點C,過點D作⊙O 的切線DE交BC于點E.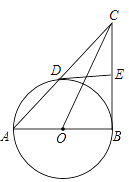
(1)求證:BE=CE;
(2)若DE平行AB,求sin∠ACO 的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com