

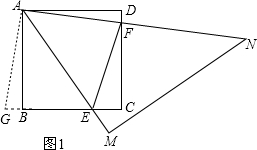
 (1)①證明:延長CB到G,使BG=DF,連接AG,
(1)①證明:延長CB到G,使BG=DF,連接AG,
|
|
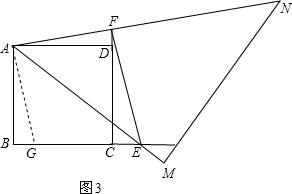 證明:在BC上取BG=DF,連接AG,
證明:在BC上取BG=DF,連接AG,
|
|


科目:初中數學 來源: 題型:
 21、如圖,在正方形網格上的一個△ABC.(其中點A、B、C均在網格上)
21、如圖,在正方形網格上的一個△ABC.(其中點A、B、C均在網格上)查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•安慶一模)如圖,等腰直角△ABC沿MN所在的直線以2cm/min的速度向右作勻速運動.如果MN=2AC=4cm,那么△ABC和正方形XYMN重疊部分的面積S(cm2)與勻速運動所用時間t(min)之間的函數的大致圖象是( )
(2012•安慶一模)如圖,等腰直角△ABC沿MN所在的直線以2cm/min的速度向右作勻速運動.如果MN=2AC=4cm,那么△ABC和正方形XYMN重疊部分的面積S(cm2)與勻速運動所用時間t(min)之間的函數的大致圖象是( )查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com