
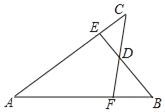
【題目】如圖,已知AB=AC,AE=AF,BE與CF交于點D,則對于下列結論:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分線上.其中正確的是( )
A. ① B. ② C. ①和② D. ①②③
【答案】D
【解析】
如圖,證明△ABE≌△ACF,得到∠B=∠C;證明△CDE≌△BDF;證明△ADC≌△ADB,得到∠CAD=∠BAD;即可解決問題.
解:如圖,連接AD;
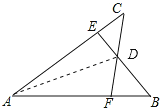
在△ABE與△ACF中,
AB=AC,∠EAB=∠FAC,AE=AF,
∴△ABE≌△ACF(SAS);
∴∠B=∠C,
∵AB=AC,AE=AF,
∴BF=CE,
在△CDE和與△BDF中,
∠B=∠C,∠BDF=∠CDE,BF=CE,
∴△CDE≌△BDF(AAS),
∴DC=DB;
在△ADC與△ADB中,
AC=AB,∠C=∠B,DC=DB,
∴△ADC≌△ADB(SAS),
∴∠CAD=∠BAD;
綜上所述,①②③均正確,
故選D.
“點睛”該題主要考查了全等三角形的判定及其性質的應用問題:應牢固掌握全等三角形的判定及其性質定理,這是靈活運用解題的基礎.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
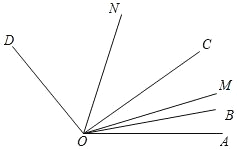
【題目】如圖,已知∠AOD=150°,OB、OC、OM、ON 是∠AOD 內的射線,若∠BOC=20°,∠AOB=10°,OM 平分∠AOC,ON 平分∠BOD,當∠BOC 在∠AOD 內繞著點 O以 3°/秒的速度逆時針旋轉 t 秒時,當∠AOM:∠DON=3:4 時,則 t=____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知數軸上兩點A,B對應的數分別是﹣1,3,點P為數軸上的一動點,其對應的數為x

(1)A、B兩點的距離AB= ;
(2)在數軸上是否存在點P,使PA+PB=6?若存在,請求出x的值;若不存在,請說明理由.
(3)如圖2,若點P以每秒1個單位的速度從點O出發向右運動,同時點A以每秒5個單位的速度向左運動,點B以每秒20個單位的速度向右運動,在運動的過程中,M、N分別是AP、OB的中點,問:![]() 的值是否發生變化?請說明理由.
的值是否發生變化?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知整數a1,a2,a3,a4,…滿足下列條件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此類推,則a2018的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點B,F,C,E在直線l上(F,C之間不能直接測量),點A,D在l異側,測得AB=DE,AC=DF,BF=EC.

(1)求證:△ABC≌△DEF;
(2)指出圖中所有平行的線段,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2017·河北遷安一模)如圖,在Rt△ABC中,直角邊AC=7 cm,BC=3 cm,CD為斜邊AB上的高,點E從點B出發沿直線BC以2 cm/s的速度移動,過點E作BC的垂線交直線CD于點F.
(1)試說明:∠A=∠BCD;
(2)點E運動多長時間,CF=AB?并說明理由.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形紙片ABCD中,對角線AC、BD交于點O,折疊正方形紙片ABCD,使AD落在BD上,點A恰好與BD上的點F重合,展開后折痕DE分別交AB、AC于點E、G,連結GF,給出下列結論:①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四邊形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,則正方形ABCD的面積是6+4 ![]() ,其中正確的結論個數為( )
,其中正確的結論個數為( ) 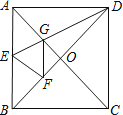
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下表為某個雨季水庫管理員記錄的水庫一周內的水位變化情況,警戒水位為150m(上周末的水位剛好達到警戒水位).
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
增減/m | +1.2 | +0.4 | +0.8 | ﹣0.1 | +0.7 | ﹣0.7 | ﹣1.1 |
注:正數表示比前一天水位上升,負數表示比前一天水位下降.
(1)本周哪一天水位最高?有多少米?
(2)本周哪一天水位最低?有多少米?
(3)根據給出的數據,以警戒水位為0點,用折線統計圖表示本周內該水庫的水位情況.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com