
【題目】如圖,在平面直角坐標系xoy中,E(8,0),F(0 , 6).
(1)當G(4,8)時,則∠FGE= °
(2)在圖中的網格區域內找一點P,使∠FPE=90°且四邊形OEPF被過P點的一條直線分割成兩部分后,可以拼成一個正方形.
要求:寫出點P點坐標,畫出過P點的分割線并指出分割線(不必說明理由,不寫畫法).

【答案】(1)90;(2)作圖見解析,P(7,7),PH是分割線.
【解析】
試題(1)根據勾股定理求出△FEG的三邊長,根據勾股定理逆定理可判定△FEG是直角三角形,且∠FGE="90" °.
(2)一方面,由于∠FPE=90°,從而根據直徑所對圓周角直角的性質,點P在以EF為直徑的圓上;另一方面,由于四邊形OEPF被過P點的一條直線分割成兩部分后,可以拼成一個正方形,從而OP是正方形的對角線,即點P在∠FOE的角平分線上,因此可得P(7,7),PH是分割線.
試題解析:(1)連接FE,
∵E(8,0),F(0 , 6),G(4,8),
∴根據勾股定理,得FG=![]() ,EG=
,EG=![]() ,FE=10.
,FE=10.
∵![]() ,即
,即![]() .
.
∴△FEG是直角三角形,且∠FGE=90 °.
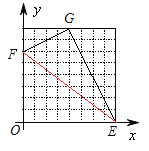
(2)作圖如下:
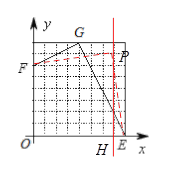
P(7,7),PH是分割線.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=x2+bx+c與x軸交A(﹣1,0)B(3,0)兩點,直線l與拋物線交于A,C兩點,其中C點的橫坐標為2.
(1)求拋物線的解析式;
(2)求直線AC的函數表達式;
(3)若點M是線段AC上的點(不與A,C重合),過M作MF∥y軸交拋物線于F,交x軸于點H,設點M的橫坐標為m,連接FA,FC,是否存在m,使△AFC的面積最大?若存在,求m的值;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現在,共享單車已遍布深圳街頭,其中較為常見的共享單車有“A.摩拜單車”、“B.小藍單車”、“C.OFO單車”、“D.小鳴單車”、“E.凡騎綠暢”等五種類型.為了解市民使用這些共享單車的情況,某數學興趣小組隨機統計部分正在使用這些單車的市民,并將所得數據繪制出了如下兩幅不完整的統計圖表 (圖1、圖2):
根據所給信息解答下列問題:
(1)此次統計的人數為人;根據已知信息補全條形統計圖;
(2)在使用單車的類型扇形統計圖中,使用E 型共享單車所在的扇形的圓心角為度;
(3)據報道,深圳每天有約200余萬人次使用共享單車,則其中使用E型共享單車的約有萬人次.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AD是高,CE是中線,點G是CE的中點,DG⊥CE,點G為垂足. 
(1)求證:DC=BE;
(2)若∠AEC=66°,求∠BCE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD是平行四邊形,則下列結論中不正確的是( )

A. 當AB=BC時,四邊形ABCD是菱形
B. 當AC⊥BD時,四邊形ABCD是菱形
C. 當∠ABC=90°時,四邊形ABCD是矩形
D. 當AC=BD時,四邊形ABCD是正方形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線m⊥n.在平面直角坐標系xOy中,x軸∥m,y軸∥n.如果以O1為原點,點A 的坐標為(1,1).將點O1平移2 ![]() 個單位長度到點O2 , 點A的位置不變,如果以O2為原點,那么點A的坐標可能是( )
個單位長度到點O2 , 點A的位置不變,如果以O2為原點,那么點A的坐標可能是( )
A.(3,﹣1)
B.(1,﹣3)
C.(﹣2,﹣1)
D.(2 ![]() +1,2
+1,2 ![]() +1)
+1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,PC切⊙O于點C,AB的延長線與PC交于點P,PC的延長線與AD交于點D,AC平分∠DAB. 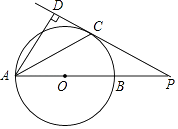
(1)求證:AD⊥PC;
(2)連接BC,如果∠ABC=60°,BC=2,求線段PC的長. 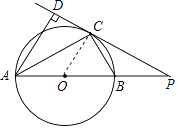
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com