
【題目】如圖,AB是⊙O的一條弦,點C是⊙O上一動點,且∠ACB=30°,點E、F分別是AC、BC的中點,直線EF與⊙O交于G、H兩點,若⊙O的半徑為10,則GE+FH的最大值為( )
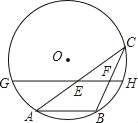
A. 5 B. 10 C. 15 D. 20
【答案】C
【解析】
首先連接OA、OB,根據圓周角定理,求出∠AOB=2∠ACB=60°,進而判斷出△AOB為等邊三角形;然后根據⊙O的半徑為5,可得AB=OA=OB=5,再根據三角形的中位線定理,求出EF的長度;最后判斷出當弦GH是圓的直徑時,它的值最大,進而求出GE+FH的最大值是多少即可.
如圖1,連接OA、OB,
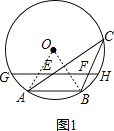 ,
,
∵∠ACB=30°,
∴∠AOB=2∠ACB=60°,
∵OA=OB,
∴△AOB為等邊三角形,
∵⊙O的半徑為10,
∴AB=OA=OB=10,
∵點E,F分別是AC、BC的中點,
∴EF=![]() AB=5,
AB=5,
要求GE+FH的最大值,即求GE+FH+EF(弦GH)的最大值,
∵當弦GH是圓的直徑時,它的最大值為:10×2=20,
∴GE+FH的最大值為:20-5=15.
故選C.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在足夠大的空地上有一段長為![]() 米的舊墻
米的舊墻![]() ,某人利用舊墻和木欄圍成一個矩形菜園
,某人利用舊墻和木欄圍成一個矩形菜園![]()
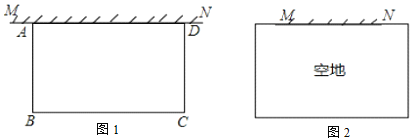
(1)如圖1其中![]() ,已知矩形菜園的一邊靠墻,另三邊一共用了
,已知矩形菜園的一邊靠墻,另三邊一共用了![]() 米木欄.
米木欄.
①若![]() ,所圍成的矩形菜園的面積為
,所圍成的矩形菜園的面積為![]() 平方米,求所利用舊墻
平方米,求所利用舊墻![]() 的長;
的長;
②求矩形菜園![]() 面積的最大值.
面積的最大值.
(2)如圖2,若![]() ,則舊墻與木欄能圍成的矩形菜園
,則舊墻與木欄能圍成的矩形菜園![]() 面積的最大值是多少?
面積的最大值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)閱讀理解:實數![]() ,
, ![]() ,∵
,∵![]() ,∴
,∴![]() ,即
,即![]() 。若
。若![]() (
(![]() 為定值),則
為定值),則![]() ,當且僅當
,當且僅當![]() 時等式成立,即
時等式成立,即![]() 時,
時, ![]() ,∴當
,∴當![]() 時,
時, ![]() 取得 值(填“最大”或“最小”)。
取得 值(填“最大”或“最小”)。
(2)理解應用:函數![]() ,當x= 時,
,當x= 時, ![]() 。
。
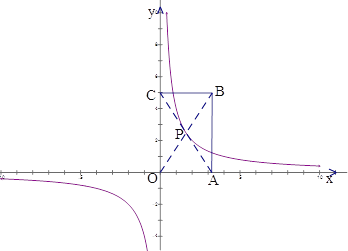
(3)拓展應用:如圖,雙曲線![]() 經過矩形OABC的對角線交點P,求矩形OABC的最小周長。
經過矩形OABC的對角線交點P,求矩形OABC的最小周長。
查看答案和解析>>
科目:初中數學 來源: 題型:
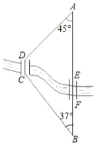
【題目】如圖,A,B兩地之間有條河,原來從A地到B地需要經過橋DC,沿折線A→D→C→B到達,現在新建了橋EF,可直接沿直線AB從A地到達B地.已知BC=11km,∠A=45°,∠B=37°,橋DC和AB平行,橋DC與橋EF的長相等.
(1)求點D到直線AB的距離;
(2)現在從A地到B地可比原來少走多少路程?
(結果保留小數點后一位.參考數據:![]() ≈1.41,sin37°≈0.60,cos37°≈0.80).
≈1.41,sin37°≈0.60,cos37°≈0.80).
查看答案和解析>>
科目:初中數學 來源: 題型:
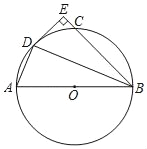
【題目】如圖,AB為⊙O的直徑,C為⊙O上一點,∠ABC的平分線交⊙O于點D,DE⊥BC于點E.
(1)試判斷DE與⊙O的位置關系,并說明理由;
(2)若⊙O的半徑為3,BC=4,求CE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有四張正面分別標有數字﹣1,0,1,2的不透明卡片,它們除數字外其余全部相同,現將它們背面朝上洗均勻.
(1)隨機抽取一張卡片,求抽到數字“﹣1”的概率;
(2)隨機抽取一張卡片,然后不放回,再隨機抽取一張卡片,請用列表或畫樹狀圖的方法求出第一次抽到數字“2”且第二次抽到數字“0”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】城市中“打車難”一直是人們關注的一個社會熱點問題.近幾年來,“互聯網+”戰略與傳統出租車行業深度融合,“優步”、“滴滴出行”等打車軟件就是其中典型的應用,名為“數據包絡分析”(簡稱DEA)的一種效率評價方法,可以很好地優化出租車資源配置,為了解出租車資源的“供需匹配”,北京、上海等城市對每天24個時段的DEA值進行調查,調查發現,DEA值越大,說明匹配度越好.在某一段時間內,北京的DEA值y與時刻t的關系近似滿足函數關系![]() (a,b,c是常數,且
(a,b,c是常數,且![]() ≠0),如圖記錄了3個時刻的數據,根據函數模型和所給數據,當“供需匹配”程度最好時,最接近的時刻t是( )
≠0),如圖記錄了3個時刻的數據,根據函數模型和所給數據,當“供需匹配”程度最好時,最接近的時刻t是( )
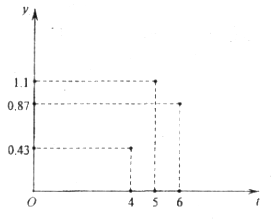
A. 4.8 B. 5 C. 5.2 D. 5.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c經過點(﹣1,0),對稱軸l如圖所示,則下列結論:①abc>0;②a﹣b+c=0;③2a+c<0;④a+b<0,其中所有正確的結論是( )

A.①③ B.②③ C.②④ D.②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com