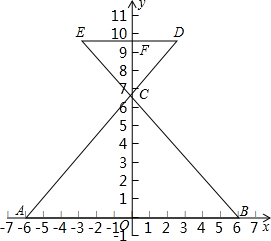
解:(1)∵A(-6,0),B(6,0),C(0,m),
∴OA=OB=6,OC=m,AB=12,
∵DE∥AB,
∴△ABC∽△DEC,
∴
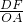
=

=

=

,
∴DF=

OA=3,CF=

OC=

m,
∴OF=

m,
則D的坐標(biāo)是(3,

m).
(2)∵C點(diǎn)關(guān)于直線DE的對稱點(diǎn)F,
又∵DE關(guān)于y軸對稱,
∴四邊形CDFE是菱形.
∴直線y=kx+b將四邊形CDFE分成周長相等的兩個四邊形,則一定經(jīng)過點(diǎn)F(0,

),
根據(jù)題意得:
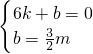
,
解得:
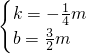
,
則直線的解析式是:y=-

mk+

m;
(3)∵△ABC為等腰三角形,
∴A、B關(guān)于y軸對稱,
∴直線AD與y軸的交點(diǎn)C就是點(diǎn)P,坐標(biāo)是(0,m).
故答案是:(3,

m);(0,m).
分析:(1)易證△ABC∽△DEC,根據(jù)相似三角形的對應(yīng)邊的比相等即可求得DF,OF的長,則D的坐標(biāo)即可求解;
(2)易證四邊形CDFE是菱形,則直線y=kx+b將四邊形CDFE分成周長相等的兩個四邊形,則一定經(jīng)過點(diǎn)F(0,

),利用待定系數(shù)法即可求得直線的解析式;
(3)△ABC為等腰三角形,則A、B關(guān)于y軸對稱,因而直線AD與y軸的交點(diǎn)C就是點(diǎn)P,據(jù)此即可求解.
點(diǎn)評:本題考查了相似三角形的判定與性質(zhì),以及待定系數(shù)法求函數(shù)的解析式,以及軸對稱的性質(zhì),正確判斷四邊形CDFE是菱形是關(guān)鍵.

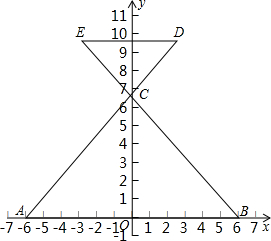 如圖,在平面直角坐標(biāo)系中,△ABCS三個頂點(diǎn)的坐標(biāo)分別為A(-6,0),B(6,0),C(0,m)(其中m>0),延長AC到點(diǎn)D,使CD=
如圖,在平面直角坐標(biāo)系中,△ABCS三個頂點(diǎn)的坐標(biāo)分別為A(-6,0),B(6,0),C(0,m)(其中m>0),延長AC到點(diǎn)D,使CD= AC,過點(diǎn)D作DE∥AB交BC的延長線于點(diǎn)E.
AC,過點(diǎn)D作DE∥AB交BC的延長線于點(diǎn)E. 解:(1)∵A(-6,0),B(6,0),C(0,m),
解:(1)∵A(-6,0),B(6,0),C(0,m),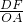 =
= =
= =
= ,
, OA=3,CF=
OA=3,CF= OC=
OC= m,
m, m,
m, m).
m). ),
),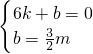 ,
,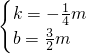 ,
, mk+
mk+ m;
m; m);(0,m).
m);(0,m). ),利用待定系數(shù)法即可求得直線的解析式;
),利用待定系數(shù)法即可求得直線的解析式;

 能考試全能100分系列答案
能考試全能100分系列答案
 如圖,在平面直角坐標(biāo)中,四邊形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,點(diǎn)P為x軸上的一個動點(diǎn),但是點(diǎn)P不與點(diǎn)0、點(diǎn)A重合.連接CP,D點(diǎn)是線段AB上一點(diǎn),連接PD.
如圖,在平面直角坐標(biāo)中,四邊形OABC是等腰梯形,CB∥OA,OA=7,AB=4,∠COA=60°,點(diǎn)P為x軸上的一個動點(diǎn),但是點(diǎn)P不與點(diǎn)0、點(diǎn)A重合.連接CP,D點(diǎn)是線段AB上一點(diǎn),連接PD. (2012•渝北區(qū)一模)如圖,在平面直角坐標(biāo)xoy中,以坐標(biāo)原點(diǎn)O為圓心,3為半徑畫圓,從此圓內(nèi)(包括邊界)的所有整數(shù)點(diǎn)(橫、縱坐標(biāo)均為整數(shù))中任意選取一個點(diǎn),其橫、縱坐標(biāo)之和為0的概率是
(2012•渝北區(qū)一模)如圖,在平面直角坐標(biāo)xoy中,以坐標(biāo)原點(diǎn)O為圓心,3為半徑畫圓,從此圓內(nèi)(包括邊界)的所有整數(shù)點(diǎn)(橫、縱坐標(biāo)均為整數(shù))中任意選取一個點(diǎn),其橫、縱坐標(biāo)之和為0的概率是 如圖,在平面直角坐標(biāo)中,等腰梯形ABCD的下底在x軸上,且B點(diǎn)坐標(biāo)為(4,0),D點(diǎn)坐標(biāo)為(0,3),則AC長為
如圖,在平面直角坐標(biāo)中,等腰梯形ABCD的下底在x軸上,且B點(diǎn)坐標(biāo)為(4,0),D點(diǎn)坐標(biāo)為(0,3),則AC長為 如圖,在平面直角坐標(biāo)xOy中,已知點(diǎn)A(-5,0),P是反比例函數(shù)y=
如圖,在平面直角坐標(biāo)xOy中,已知點(diǎn)A(-5,0),P是反比例函數(shù)y= ∠COA=45°,動點(diǎn)P從點(diǎn)O出發(fā),在梯形OABC的邊上運(yùn)動,路徑為O→A→B→C,到達(dá)點(diǎn)C時停止.作直線CP.
∠COA=45°,動點(diǎn)P從點(diǎn)O出發(fā),在梯形OABC的邊上運(yùn)動,路徑為O→A→B→C,到達(dá)點(diǎn)C時停止.作直線CP.