
【題目】定義一種對正整數n的“F”運算:①當n為奇數時,F(n)=3n+1;②當n為偶數時,F(n)=![]() (其中k是使F(n)為奇數的正整數)……,兩種運算交替重復進行,例如,取n=24,則:若n=13,則第2018次“F”運算的結果是_____.
(其中k是使F(n)為奇數的正整數)……,兩種運算交替重復進行,例如,取n=24,則:若n=13,則第2018次“F”運算的結果是_____.
![]()
 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
【題目】隨著互聯網的普及,某手機廠商采用先網絡預定,然后根據訂單量生產手機的方式銷售,2015年該廠商將推出一款新手機,根據相關統計數據預測,定價為2200元,日預訂量為20000臺,若定價每減少100元,則日預訂量增加10000臺.
(1)設定價減少x元,預訂量為y臺,寫出y與x的函數關系式;
(2)若每臺手機的成本是1200元,求所獲的利潤w(元)與x(元)的函數關系式,并說明當定價為多少時所獲利潤最大;
(3)若手機加工廠每天最多加工50000臺,且每批手機會有5%的故障率,通過計算說明每天最多接受的預訂量為多少?按最大量接受預訂時,每臺售價多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
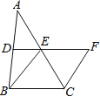
【題目】圖,在△ABC中,D、E分別是AB、AC的中點,BE=2DE,延長DE到F,使得EF=BE,連接CF.
(1)求證:四邊形BCFE是菱形.
(2)若DE=4cm,∠EBC=60°,求菱形BCFE的面積。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“元旦”期間,某文具店購進100只兩種型號的文具進行銷售,其進價和售價如下
型號 | 進價(元/只) | 售價(元/只) |
A型 | 10 | 12 |
B型 | 15 | 23 |
(1)該店用1300元可以購進A,B兩種型號的文具各多少只?
(2)若把所購進A,B兩種型號的文具全部銷售完,利潤率超過40%沒有?請你說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,D為AB邊上一點,E為CD中點,AC=![]() ,∠ABC=30°,∠A=∠BED=45°,則BD的長為( )
,∠ABC=30°,∠A=∠BED=45°,則BD的長為( )

A. ![]() B.
B. ![]() +1﹣
+1﹣![]() C.
C. ![]() ﹣
﹣![]() D.
D. ![]() ﹣1
﹣1
查看答案和解析>>
科目:初中數學 來源: 題型:
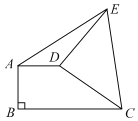
【題目】如圖 ,直角梯形 ABCD 中, AD ∥ BC , AB ⊥ BC,AD 2 ,將腰CD 以點 D 為中心逆時針旋轉 90°至 DE ,連接 AE、CE ,△ADE 的面積為 3,則 BC 的長為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有三個有理數x,y,z,若x=![]() ,且x與y互為相反數,y是z的倒數.
,且x與y互為相反數,y是z的倒數.
(1)當n為奇數時,你能求出x,y,z這三個數嗎?當n為偶數時,你能求出x,y,z,這三個數嗎?若能,請計算并寫出結果;若不能,請說明理由.
(2)根據(1)的結果計算:xy﹣yn﹣(y﹣z)2019的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
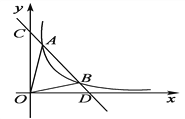
【題目】如圖,一次函數y=kx+b與反比例函數y=![]() (x>0)的圖象交于A(m,6),B(3,n)兩點.
(x>0)的圖象交于A(m,6),B(3,n)兩點.
(1)求一次函數的解析式;
(2)根據圖象直接寫出kx+b-![]() <0時x的取值范圍;
<0時x的取值范圍;
(3)求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為民中學租用兩輛速度相同的小汽車送1名帶隊老師和6名學生到城區中學參加數學競賽,每輛限坐4人(不包括司機).其中一輛小汽車在距離考場16.5 km的地方出現故障,此時離截止進考場的時刻還有50分鐘,這時唯一可利用的交通工具是另一輛小汽車,且這輛車的平均速度是55 km/h,人步行的速度是5 km/h(上、下車時間忽略不計).
(1)若小汽車送4人到達考場,然后再回到出故障處接其他人,請你通過計算說明他們能否在截止進考場的時刻前到達考場;
(2)假如你是帶隊的老師,請設計一種你認為較優的運送方案,使他們能在截止進考場的時刻前到達考場,并通過計算說明方案的可行性.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com