
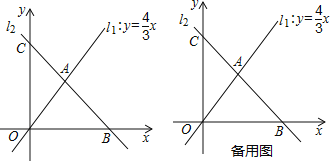
【題目】如圖,直線![]() 與直線
與直線![]() 交于點
交于點![]() ,直線
,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() 、點
、點![]() .
.
(1)求直線![]() 的關系式;
的關系式;
(2)若與![]() 軸平行的直線
軸平行的直線![]() 與直線
與直線![]() 分別交于點
分別交于點![]() 、點
、點![]() ,則
,則![]() 的面積為_____(直接填空);
的面積為_____(直接填空);
(3)在(2)的情況下,把![]() 沿著過原點的直線
沿著過原點的直線![]() 翻折,當點
翻折,當點![]() 落在直線
落在直線![]() 上時,直接寫出
上時,直接寫出![]() 的值.
的值.
【答案】(1)![]() ;(2)14;(3)
;(2)14;(3)![]() 或
或![]() .
.
【解析】
(1)利用一次函數圖象上點的坐標特征可求出點A的坐標,由點A的坐標,再利用待定系數法即可求出直線l2的解析式;
(2)利用一次函數圖象上點的坐標特征可求出點B,M,N的坐標,再利用三角形的面積公式即可求出△BMN的面積;
(3)設翻折后點A落在點F處,連接AF交折線于點P,由折痕所在直線的解析式可設直線AF的解析式為y=-![]() x+d,由點A的坐標,利用待定系數法可求出直線AF的解析式,代入x=8可求出點F的坐標,由折疊的性質結合點A,F的坐標可求出點P的坐標,再利用一次函數圖象上點的坐標特征可得出關于k的方程,解之即可得出結論.
x+d,由點A的坐標,利用待定系數法可求出直線AF的解析式,代入x=8可求出點F的坐標,由折疊的性質結合點A,F的坐標可求出點P的坐標,再利用一次函數圖象上點的坐標特征可得出關于k的方程,解之即可得出結論.
(1)將A(6,a)代入y=![]() x,得:a=
x,得:a=![]() ×6,
×6,
∴a=8,
∴點A的坐標為(6,8).
將A(6,8)代入y=-x+b,得:8=-6+b,
∴b=14,
∴直線l2的解析式為y=-x+14.
(2)當x=8時,y=![]() x=
x=![]() ,y=-x+14=6,
,y=-x+14=6,
∴點M的坐標為(8,![]() ),點N的坐標為(8,6).
),點N的坐標為(8,6).
當y=0時,-x+14=0,
解得:x=14,
∴點B的坐標為(14,0).
設直線x=8與x軸的交點為E,則點E的坐標為(8,0),如圖1所示.

∴S△BMN=![]() BEMN=
BEMN=![]() ×(14-8)×(
×(14-8)×(![]() -6)=14.
-6)=14.
故答案為14.
(3)設翻折后點A落在點F處,連接AF交折痕所在的直線于點P,如圖2所示.
∵折痕所在直線的解析式為y=kx(k≠0),
∴設直線AF的解析式為y=-![]() x+d,
x+d,
將A(6,8)代入y=-![]() x+d,得:8=-
x+d,得:8=-![]() +d,
+d,
∴d=8+![]() ,
,
∴直線AF的解析式為y=-![]() x+8+
x+8+![]() .
.
當x=8時,y=-![]() x+8+
x+8+![]() =8-
=8-![]() ,
,
∴點F的坐標為(8,8-![]() ).
).
又∵點P為線段AF的中點,
∴點P的坐標為(![]() ,
, ),即(7,8-
),即(7,8-![]() ).
).
將P(7,8-![]() )代入y=kx,得:8-
)代入y=kx,得:8-![]() =7k,
=7k,
整理,得:7k2-8k+1=0,
解得:k1=1,k2=![]() ,
,
∴k的值為1或![]() .
.


科目:初中數學 來源: 題型:
【題目】菱形![]() 中,
中,![]() 為邊
為邊![]() 上的點,
上的點,![]() 相交于點
相交于點![]() .
.
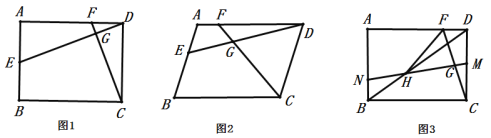
(1)如圖1,若![]() ,
,![]() ,求證:
,求證:![]() ;
;
(2)如圖2,若![]() .求證:
.求證:![]() ;
;
(3)如圖3,在(1)的條件下,平移線段![]() 到
到![]() ,使
,使![]() 為
為![]() 的中點,連接
的中點,連接![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,請直接寫出
,請直接寫出![]() 的長度.
的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】家庭過期藥品屬于“危險廢物”,處理不當將污染環境,危害健康某市藥監部門為了解家庭處理過期藥品的方式,決定對全市家庭作一次簡單隨機抽樣調查.
(1)下列選取樣本的方法最合理的一種是 (只需填上正確答案的序號)
①在市中心某個居民區以家庭為單位隨機抽取;
②在全市醫務工作者中以家庭為單位隨機抽取;
③在全市常住人口中以家庭為單位隨機抽取.
(2)本次抽樣調查發現,接受調查的家庭都有過期藥品,現將有關數據呈現如下圖:
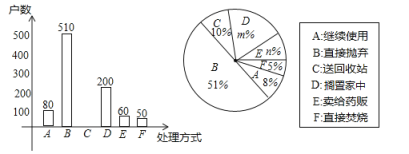
①![]() ,
,
②補全條形統計圖;(標上數據)
③家庭過期藥品的正確處理方式是送回收站,若該市有![]() 萬戶家庭,請估計大約有多少戶家庭處理過期藥品的方式是送回收站.
萬戶家庭,請估計大約有多少戶家庭處理過期藥品的方式是送回收站.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】初中學生對待學習的態度一直是教育工作者極為關注的一個問題.為此某市教育局對本市部分學校的八年級學生對待學習的態度進行了一次抽樣調查(把學習態度分為三個層級,A級:喜歡;B級:不太喜歡;C級:不喜歡),并將調查結果繪制成不完整的統計圖(如圖![]() ).請根據圖中提供的信息,解答下列問題:
).請根據圖中提供的信息,解答下列問題:
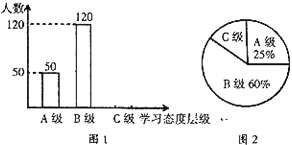
(1)此次抽樣調查中,共調查了_____名學生;
(2)將條形統計圖補充完整;
(3)求出扇形統計圖中![]() 級所占的圓心角的度數;
級所占的圓心角的度數;
(4)根據抽樣調查結果,請你估計該市近![]() 名初中生中大約有多少名學生學習態度達標.(達標包括
名初中生中大約有多少名學生學習態度達標.(達標包括![]() 級和
級和![]() 級)
級)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, ![]() 是直線
是直線![]() 上的兩點,直線l1、l2的初始位置與直線
上的兩點,直線l1、l2的初始位置與直線![]() 重合將l1繞點
重合將l1繞點![]() 順時針以每秒10°的速度旋轉,將l2繞點B逆時針以每秒5°的速度旋轉,且兩條直線從重合位置同時開始旋轉,設旋轉時間為
順時針以每秒10°的速度旋轉,將l2繞點B逆時針以每秒5°的速度旋轉,且兩條直線從重合位置同時開始旋轉,設旋轉時間為![]() 秒(
秒(![]() 是正整數).當
是正整數).當![]() 時,設
時,設![]() 的交點為
的交點為![]() ;當
;當![]() 時,設
時,設![]() 的交點為
的交點為![]() ;當
;當![]() 時設
時設![]() 的交點為
的交點為![]() ……那么當
……那么當![]() 時,
時, ![]() 相交所得的鈍角是__________.當
相交所得的鈍角是__________.當![]() 落在
落在![]() 上方時,
上方時, ![]() 的最小值是__________.
的最小值是__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在正方形ABCD外取一點E,連接AE、BE、DE.過點A作AE的垂線交DE于點P.若AE=AP=1,PB=![]() .下列結論:①△APD≌△AEB;②點B到直線AE的距離為
.下列結論:①△APD≌△AEB;②點B到直線AE的距離為![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正確結論的序號是( )
.其中正確結論的序號是( )

A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠的甲、乙兩個車間各生產了400個新款產品,為了檢驗甲、乙兩車間生產的同一款新產品的合格情況(尺寸范圍在165≤x<180為合格),分別從甲、乙兩個車間生產的產品中隨機各抽取了20個樣品迸行檢測,獲得了它們的數據(尺寸),并對數據進行了整理、描述和分析.下面給出了部分信息:
a.甲車間產品尺寸的扇形統計圖如下(數據分為6組:165≤x<170,170≤x<175,
175≤x<180,180≤x<185,185≤x<190,190≤x≤195):


b.甲車間生產的產品尺寸在175≤x<180這一組的是:
175 176 176 177 177 178 178 179 179
c.甲、乙兩車間生產產品尺寸的平均數、中位數、眾數如下:
車間 | 平均數 | 中位數 | 眾數 |
甲車間 | 178 | m | 183 |
乙車間 | 177 | 182 | 184 |
根據以上信息,回答下列問題:
(1)表中m的值為 ;
(2)此次檢測中,甲、乙兩車間生產的產品合格率更高的是 (填“甲”或“乙”),理由是 ;
(3)如果假設這個工廠生產的所有產品都參加了檢測,那么估計甲車間生產該款新產品中合格產品有 個.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com