
在平面直角坐標系中,已知函數 和函數
和函數 ,不論
,不論 取何值,
取何值, 都取
都取 與
與 二者之中的較小值.
二者之中的較小值.
1.求 關于
關于 的函數關系式
的函數關系式
2.現有二次函數 ,若函數
,若函數 和
和 都隨著
都隨著 的增大而減小,求自變
的增大而減小,求自變
量 的取值范圍
的取值范圍
3.在(2)的結論下,若函數 和
和 的圖象有且只有一個公共點,求
的圖象有且只有一個公共點,求 的取值范圍.
的取值范圍.
1.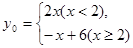 ……………………………………….……..2分
……………………………………….……..2分
(說明:兩個自變量取值范圍都含有等號或其中一個含等號均不扣分,都沒等號扣1分)
2. 對函數
對函數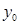 ,當
,當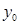 隨
隨 的增大而減小,
的增大而減小,
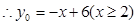 ,
………………………………………..…….3分
,
………………………………………..…….3分
又 函數
函數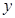 的對稱軸為直線
的對稱軸為直線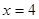 ,
…………………………….……..4分
,
…………………………….……..4分
且 ,
,
 當
當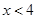 時,
時,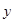 隨
隨 的增大而減小,
………………………….……..5分
的增大而減小,
………………………….……..5分

 …………………………………….…………….…..6分
…………………………………….…………….…..6分
3.①若函數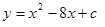 與
與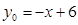 只有一個交點,且交點在
只有一個交點,且交點在 范圍內.
范圍內.
則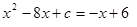 ,
,
 ,
,
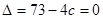 ,
,
得 …………………………….…………….…7分
…………………………….…………….…7分
此時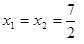 ,符合
,符合 , ………….…………..….…8分
, ………….…………..….…8分

②若函數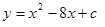 與
與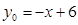 有兩個交點,其中一個在
有兩個交點,其中一個在 范圍內,另一個交點在
范圍內,另一個交點在 范圍外.則
范圍外.則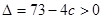 , 即
, 即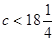 , ………….…9分
, ………….…9分
方法一: 對
對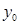 ,當
,當 時
時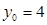 ;當
;當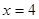 時
時 .
.
又 當
當 時,
時,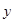 隨
隨 的增大而減小,
……….………10分
的增大而減小,
……….………10分
若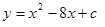 與
與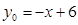 在
在 內有一個交點,
內有一個交點,
則當 時
時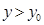 ;當
;當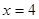 時
時 ,
,
即當 時
時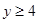 ;當
;當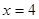 時
時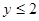 .
.
也即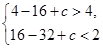 解得
解得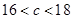 ,
……….……..…11分
,
……….……..…11分
由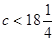 ,得
,得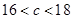 …………………………..…12分
…………………………..…12分
綜上所述,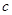 的取值范圍是:
的取值范圍是: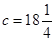 或
或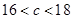 .
.
方法二:由函數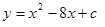 與
與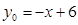 的一個交點在
的一個交點在 范圍內,另一個交點在
范圍內,另一個交點在 范圍外,可得:
范圍外,可得: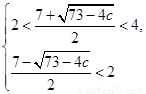 或
或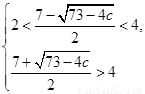
解第一個不等式組,可得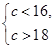 即無解;
…….………10分
即無解;
…….………10分
解第二個不等式組,可得 即
即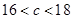 ,
….………11分
,
….………11分
由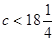 ,得
,得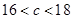 .
……………………………..…12分
.
……………………………..…12分
【解析】(1)有題意可知y1和y2交于(2,4),當x小于2時,y1和y2中y1較小,當x大于2時,y1和y2中y2較小,當x=2時,y1=y2,因此,y0是關于x的分段函數,當x<2時,y0=-x+6,當x>2時,y0=2x
(2)因為對函數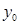 ,當
,當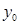 隨
隨 的增大而減小,所以y0=-x+6, 函數
的增大而減小,所以y0=-x+6, 函數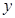 的對稱軸為直線
的對稱軸為直線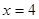 ,且
,且 ,所以自變量
,所以自變量 的取值范圍
的取值范圍
(3)分兩種情況討論:①若函數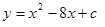 與
與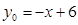 只有一個交點,且交點在
只有一個交點,且交點在 范圍內.;②若函數
范圍內.;②若函數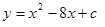 與
與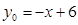 有兩個交點,其中一個在
有兩個交點,其中一個在 范圍內,另一個交點在
范圍內,另一個交點在 范圍外
范圍外


科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
 坐標原點.A、B兩點的橫坐標分別是方程x2-4x-12=0的兩根,且cos∠DAB=
坐標原點.A、B兩點的橫坐標分別是方程x2-4x-12=0的兩根,且cos∠DAB=
| ||
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 18、在平面直角坐標系中,把一個圖形先繞著原點順時針旋轉的角度為θ,再以原點為位似中心,相似比為k得到一個新的圖形,我們把這個過程記為【θ,k】變換.例如,把圖中的△ABC先繞著原點O順時針旋轉的角度為90°,再以原點為位似中心,相似比為2得到一個新的圖形△A1B1C1,可以把這個過程記為【90°,2】變換.
18、在平面直角坐標系中,把一個圖形先繞著原點順時針旋轉的角度為θ,再以原點為位似中心,相似比為k得到一個新的圖形,我們把這個過程記為【θ,k】變換.例如,把圖中的△ABC先繞著原點O順時針旋轉的角度為90°,再以原點為位似中心,相似比為2得到一個新的圖形△A1B1C1,可以把這個過程記為【90°,2】變換.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com