
【題目】(1)先完成下列表格:
a | …… | 0.0001 | 0.01 | 1 | 100 | 10000 | …… |
| …… | 0.01 | ______ | 1 | ______ | ______ | …… |
(2)由上表你發現什么規律?
(3)根據你發現的規律填空:
①已知![]() =1.732則
=1.732則![]() =______
=______![]() =______
=______
②已知![]() =0.056,則
=0.056,則![]() =______
=______
【答案】(1)0.1,10,100;(2)被開方數的小數點向左或向右每移動兩位開方后所得的結果相應的也向左或向右移動1位;(3)17.32,0.1732,560
【解析】
(1)直接利用已知數據開平方得出答案;
(2)利用原數據與開平方后的數據變化得出一般性規律是被開方數的小數點向左或向右每移動兩位開方后所得的結果相應的也向左或向右移動1位;
(3)利用(2)中發現的規律進而分別得出各數據答案.
解:(1)
a | …… | 0.0001 | 0.01 | 1 | 100 | 10000 | …… |
| …… | 0.01 | 0.1 | 1 | 10 | 100 | …… |
(2)規律是:被開方數的小數點向左或向右每移動兩位開方后所得的結果相應的也向左或向右移動1位;
(3)①∵![]() =1.732,∴
=1.732,∴![]() =17.32;
=17.32;
![]() =0.1732;
=0.1732;
②∵![]() =0.056,∴
=0.056,∴![]() =560.
=560.
故答案為:①17.32;0.1732;②560.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖所示,AB是⊙O的直徑,AD與⊙O相切于點A,DE與⊙O相切于點E,點C為DE延長線上一點,且CE=CB.
(1)求證:BC為⊙O的切線;
(2)若AB=4,AD=1,求線段CE的長.
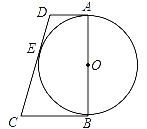
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:
如圖1,點![]() 是直線
是直線![]() 上一點,
上一點,![]() 上方的四邊形
上方的四邊形![]() 中,
中,![]() ,延長
,延長![]() ,
,![]() ,探究
,探究![]() 與
與![]() 的數量關系,并證明.
的數量關系,并證明.
小白的想法是:“作![]() (如圖2),通過推理可以得到
(如圖2),通過推理可以得到![]() ,從而得出結論”.
,從而得出結論”.
請按照小白的想法完成解答:
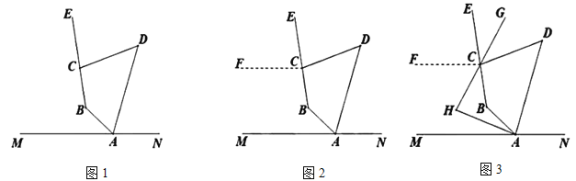
拓展延伸:
保留原題條件不變,![]() 平分
平分![]() ,反向延長
,反向延長![]() ,交
,交![]() 的平分線于點
的平分線于點![]() (如圖3),設
(如圖3),設![]() ,請直接寫出
,請直接寫出![]() 的度數(用含
的度數(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料,求值:1+2+22+23+24+…+22015.解:設S=1+2+22+23+24+…+22015,將等式兩邊同時乘以2得:2S=2+22+23+24+…+22015+22016;將下式減去上式得2S﹣S=22016﹣1;即S=1+2+22+23+24+…+22015=22016﹣1;請你仿照此法計算:
(1)1+2+22+23+…+210
(2)1+3+32+33+34+…+3n(其中n為正整數)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場將每件進價為![]() 元的某種商品原來按每件
元的某種商品原來按每件![]() 元出售,一天可售出
元出售,一天可售出![]() 件.后來經過市場調查,發現這種商品單價每降低
件.后來經過市場調查,發現這種商品單價每降低![]() 元,其銷量可增加
元,其銷量可增加![]() 件.
件.
![]() 求商場經營該商品原來一天可獲利潤多少元?
求商場經營該商品原來一天可獲利潤多少元?
![]() 若商場經營該商品一天要獲利潤
若商場經營該商品一天要獲利潤![]() 元,并讓顧客得到實惠,則每件商品應降價多少元?
元,并讓顧客得到實惠,則每件商品應降價多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為了增強學生體質,決定開設以下體育課外活動項目:A.籃球 B.乒乓球C.羽毛球 D.足球,為了解學生最喜歡哪一種活動項目,隨機抽取了部分學生進行調查,并將調查結果繪制成了兩幅不完整的統計圖,

請回答下列問題:
(1)這次被調查的學生共有多少人?
(2)請你將條形統計圖(2)補充完整;
(3)在平時的乒乓球項目訓練中,甲、乙、丙、丁四人表現優秀,現決定從這四名同學中任選兩名參加乒乓球比賽,求恰好選中甲、乙兩位同學的概率(用樹狀圖或列表法解答)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在三角形ABC中,已知AC⊥BC,CD⊥AB,∠1=∠2.對于下列五個結論:
①DE∥AC;
②∠1=∠B;
③∠3=∠A;
④∠3=∠EDB;
⑤∠2與∠3互補.
其中正確的有( )

A. 2個B. 3個C. 4個D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學組織學生春游,原計劃租用45座客車若干輛,但有15人沒有座位;若租用同樣數量的60座客車,則多出一輛車,且其余客車恰好坐滿,已知45座客車每日每輛租金為220元,60座客車每日每輛租金為300元.試問:
(1)春游學生共多少人,原計劃租45座客車多少輛?
(2)若租用同一種車,要使每位同學都有座位,怎樣租車更合算.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A(-4,n)、B(3,4)是一次函數y1=kx+b的圖象與反比例函數![]() 的圖象的兩個交點,過點D(t,0)(0<t<3)作x軸的垂線,分別交雙曲線
的圖象的兩個交點,過點D(t,0)(0<t<3)作x軸的垂線,分別交雙曲線![]() 和直線y1=kx+b于P、Q兩點
和直線y1=kx+b于P、Q兩點
(1) 直接寫出反比例函數和一次函數的解析式
(2) 當t為何值時,S△BPQ=![]() S△APQ
S△APQ
(3) 以PQ為邊在直線PQ的右側作正方形PQMN,試說明:邊QM與雙曲線![]() (x>0)始終有交點
(x>0)始終有交點

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com