
【題目】如圖![]() 、圖
、圖![]() 、圖
、圖![]() ,在矩形
,在矩形![]() 中,
中,![]() 是
是![]() 邊上的一點,以
邊上的一點,以![]() 為邊作平行四邊形
為邊作平行四邊形![]() ,使點
,使點![]() 在
在![]() 的對邊
的對邊![]() 上,
上,
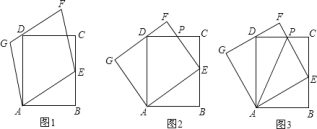
![]() 如圖
如圖![]() ,試說明:平行四邊形
,試說明:平行四邊形![]() 的面積與矩形
的面積與矩形![]() 的面積相等;
的面積相等;
![]() 如圖
如圖![]() ,若平行四邊形
,若平行四邊形![]() 是矩形,
是矩形,![]() 與
與![]() 交于點
交于點![]() ,試說明:
,試說明:![]() 、
、![]() 、
、![]() 、
、![]() 四點在同一個圓上;
四點在同一個圓上;
![]() 如圖
如圖![]() ,若
,若![]() ,平行四邊形
,平行四邊形![]() 是正方形,且
是正方形,且![]() 是
是![]() 的中點,
的中點,![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,判斷以
,判斷以![]() 為直徑的圓與直線
為直徑的圓與直線![]() 的位置關系,并說明理由.
的位置關系,并說明理由.
【答案】(1)見解析;(2)見解析;(3)以![]() 為直徑的圓與直線
為直徑的圓與直線![]() 相切,理由見解析.
相切,理由見解析.
【解析】
(1)作出AE邊上的高,分別得出長方形和平行四邊形的面積表達式,可得其結果相同,從而說明平行四邊形AEFG的面積與矩形ABCD的面積相等.
(2)先求出∠ADC=∠FEA=90°,再根據圓內接四邊形的判定定理:“如果一個四邊形的一組對角互補,那么這個四邊形內接于圓”解答.
(3)過D作DH⊥AP于H,根據∠2+∠3=90°,∠1+∠2=90°,可得∠3=∠1,可求出△ADG∽△AEB;再根據D是FG的中點可求出其相似比為2,再由△ADG與△AEB相似可得其對應邊成比例,可求出△ADG∽△AEB∽△APD;最后根據相似三角形的性質可得AD是∠GAH的平分線,可求出DG=DH,故DG=DF,即可解答.
![]() 過
過![]() 點作
點作![]() 垂直
垂直![]() 于點
于點![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
所以![]() ,
,
所以,![]() .
.
![]() 因為平行四邊形
因為平行四邊形![]() 是矩形,四邊形
是矩形,四邊形![]() 也是矩形;
也是矩形;
所以![]() ,
,
則![]() ,
,
所以![]() 、
、![]() 、
、![]() 、
、![]() 四點在同一個圓上.
四點在同一個圓上.
![]() 相切.
相切.
過![]() 作
作![]() 于
于![]() ;
;
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中點,
的中點,
∴![]() ,
,
在![]() 與
與![]() 中,
中,![]() ;
;
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]() 是
是![]() 的平分線,
的平分線,
∴![]() ,∵
,∵![]() ,
,![]() ,
,
∴以![]() 為直徑的圓與直線
為直徑的圓與直線![]() 相切.
相切.


科目:初中數學 來源: 題型:
【題目】我校八年級有800名學生,在體育中考前進行一次排球模擬測試,從中隨機抽取部分學生,根據其測試成績制作了下面兩個統計圖,請根據相關信息,解答下列問題:
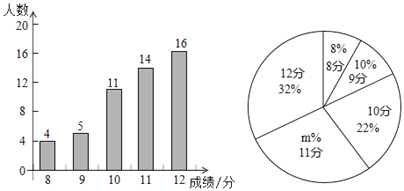
(1)本次抽取到的學生人數為________,圖2中![]() 的值為_________.
的值為_________.
(2)本次調查獲取的樣本數據的平均數是__________,眾數是________,中位數是_________.
(3)根據樣本數據,估計我校八年級模擬體測中得12分的學生約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
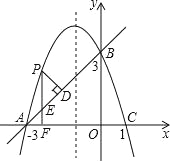
【題目】如圖,在平面直角坐標系xOy中,拋物線y=ax2+bx+c經過A、B、C三點,已知點A(﹣3,0),B(0,3),C(1,0).
(1)求此拋物線的解析式.
(2)點P是直線AB上方的拋物線上一動點,(不與點A、B重合),過點P作x軸的垂線,垂足為F,交直線AB于點E,作PD⊥AB于點D.動點P在什么位置時,△PDE的周長最大,求出此時P點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點P的坐標為(-3,4),作出點P關于x軸對稱的點P1,稱為第1次變換;再作出點P1關于y軸對稱的點P2,稱為第2次變換;再作點P2關于x軸對稱的點P3,稱為第3次變換,…,依次類推,則第2019次變換得到的點P2019的坐標為 ____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
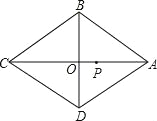
【題目】如圖,在菱形ABCD中,對角線AC、BD相交于點O.AC=8cm,BD=6cm,點P為AC上一動點,點P以1cm/的速度從點A出發沿AC向點C運動.設運動時間為ts,當t=_____s時,△PAB為等腰三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,動點P從點B出發沿射線BC以1cm/s的速度移動,設運動的時間為t秒,當△ABP為等腰三角形時,t的取值為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知如圖,拋物線y=![]() x2+
x2+![]() x﹣
x﹣![]() 與x軸交于A、B兩點(點A在點B的左側)與y軸交于點C,直線BE⊥BC與點B,與拋物線的另一交點為E.
與x軸交于A、B兩點(點A在點B的左側)與y軸交于點C,直線BE⊥BC與點B,與拋物線的另一交點為E.
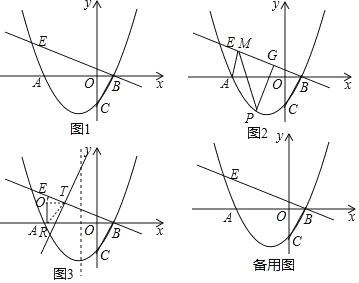
(1)如圖1,求點E的坐標;
(2)如圖2,若點P為x軸下方拋物線上一動點,過P作PG⊥BE與點G,當PG長度最大時,在直線BE上找一點M,使得△APM的周長最小,并求出周長的最小值.
(3)如圖3,將△BOC在射線BE上,設平移后的三角形為△B′O′C′,B′在射線BE上,若直線B′C′分別與x軸、拋物線的對稱軸交于點R、T,當△O′RT為等腰三角形時,求R的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在平面直角坐標系xOy中,正比例函數y=![]() x的圖象經過點A,點A的縱坐標為4,反比例函數y=
x的圖象經過點A,點A的縱坐標為4,反比例函數y=![]() 的圖象也經過點A,第一象限內的點B在這個反比例函數的圖象上,過點B作BC∥x軸,交y軸于點C,且AC=AB.求:
的圖象也經過點A,第一象限內的點B在這個反比例函數的圖象上,過點B作BC∥x軸,交y軸于點C,且AC=AB.求:

(1)這個反比例函數的解析式;
(2)直線AB的表達式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com