(2011內(nèi)蒙古赤峰,22,

12分)如圖,等圓⊙
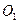
和⊙
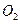
相交于A、B兩點,⊙
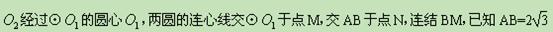
(1)求證:BM是⊙
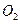
的切線;
(2)求
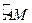
的長。

解:如圖,連結


∵⊙
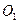
和⊙
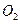
是等圓,且
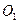
在⊙
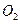
上。
∴點
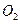
也在⊙
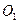
上。

∵
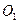
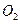
是兩圓的連心線
∴M
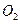
是⊙
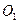
的直徑
∴∠MB
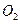
=90°
又∵直線BM經(jīng)過半徑的
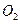
B的外端;
∴直線BM是⊙
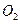
的切線
(2)連結
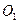
A、
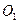
B
∵點B既在⊙
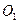
上,又在⊙
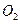
上
∴
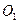
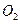
=
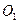
B=
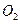
B
∴∠N
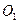
B=60°
∵
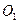
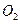
是兩圓的連心線
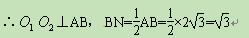
在Rt△N
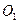
B中,sin60°=
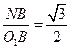
,
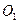
B="2"
∵
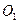
M=
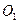
B
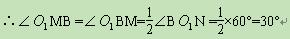
∴在Rt△MBN中,∠MBN= 60°
∴∠M
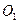
A=120°
∴

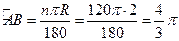
練習冊系列答案
相關習題
科目:初中數(shù)學
來源:不詳
題型:解答題
(10分)如

圖,AB是⊙O的直徑,弦DE垂直平分半徑OA,C為垂足,DE=3,
連接BD,過點E作EM∥BD,交BA的延長

線于點M.
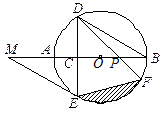
(1)求⊙O的半徑;
(2)求證:EM是⊙O的切線;
(3)若弦DF與直徑AB相交于點P,當∠APD=45º時,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:填空題
(11·丹東)已知:線段AB=3.5cm,⊙A和⊙B的半徑分別是1.5cm和4cm,則⊙A和⊙B的位置關系是____________.
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:單選題
五邊形的外角和等于
| A.180° | B.360 ° | C.540° | D.720° |
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:解答題
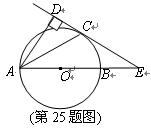
(11·柳州)(本題滿分10分)
如圖,已知
AB是⊙
O的直徑,銳角∠
DAB的平分線
AC交⊙
O于點
C,作
CD⊥
AD,垂足為
D,直線
CD與
AB的延長線交于點
E.
(1)求證:直線
CD為⊙
O的切線;
(2)當
AB=2
BE,且
CE=時,求
AD的長.
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:單選題
已知⊙O
1與⊙O
2相切,若⊙O
1的半徑為1,兩圓的圓心距為5,則⊙O
2的半徑為【 】
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:單選題
(2011?德州)一個平面封閉圖形內(nèi)(含邊界)任意兩點距離的最大值稱為該圖形的“直徑”,封閉圖形的周長與直徑之比稱為圖形的“周率”,下面四個平面圖形(依次為正三角形、正方形、正六邊形、圓)的周率從左到右依次記為a
1,a
2,a
3,a
4,則下列關系中正確的是( )
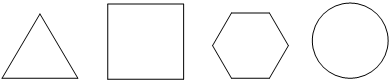
| A.a(chǎn)4>a2>a1 | B.a(chǎn)4>a3>a2 |
| C.a(chǎn)1>a2>a3 | D.a(chǎn)2>a3>a4 |
查看答案和解析>>
科目:初中數(shù)學
來源:不詳
題型:填空題
(11·漳州)兩圓的半徑分別為6和5,圓心距為10,則這兩圓的位置關系是_ ▲ .
查看答案和解析>>

 12分)如圖,等圓⊙
12分)如圖,等圓⊙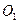 和⊙
和⊙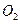 相交于A、B兩點,⊙
相交于A、B兩點,⊙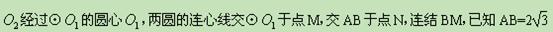
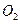 的切線;
的切線;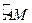 的長。
的長。
 名校課堂系列答案
名校課堂系列答案 圖,AB是⊙O的直徑,弦DE垂直平分半徑OA,C為垂足,DE=3,
圖,AB是⊙O的直徑,弦DE垂直平分半徑OA,C為垂足,DE=3, 線于點M.
線于點M.

