
【題目】如圖,在平面直角坐標系xOy中,AB∥OC,A(0,3),B(a,b),C(c,0),且a,c滿足![]() .點P從點A出發,以每秒1個單位長度的速度向點B運動,點Q從點O同時出發,以每秒2個單位長度的速度向點C運動,當點Q到達點C時,點P隨之停止運動.設運動時間為t(秒).
.點P從點A出發,以每秒1個單位長度的速度向點B運動,點Q從點O同時出發,以每秒2個單位長度的速度向點C運動,當點Q到達點C時,點P隨之停止運動.設運動時間為t(秒).

(1)B,C兩點的坐標為:B ,C ;
(2)當t為何值時,四邊形PQCB是平行四邊形?
(3)D為線段AB的中點,求當t為何值時,△ADQ是等腰三角形?
【答案】(1)![]() ,
,![]() ;(2)當t=4時,四邊形PQCB是平行四邊形;(3)當t為
;(2)當t=4時,四邊形PQCB是平行四邊形;(3)當t為![]() ,或
,或![]() ,或2,或
,或2,或![]() 時,△ADQ是等腰三角形.
時,△ADQ是等腰三角形.
【解析】
(1)根據點的坐標特點和二次根式的性質得出a,b,c的值進而得出答案;
(2)由題意得:![]() ,
,![]() ,根據平行四邊形的判定可得
,根據平行四邊形的判定可得![]() 再解方程即可;
再解方程即可;
(3)分別以AD為腰或AD為底邊時情況,根據等腰三角形的性質和勾股定理即可得到結論.
解:(1)∵![]() .
.
∴![]() ,
,
解得a=10,
∴c=14,
∵AB∥OC,A(0,3),
∴b=3,
即B(10,3),C(14,0);
故答案為:(10,3),(14,0)
(2)設運動時間為t(秒),由題意可知:
![]() ,
,![]()
又∵AB∥OC
∴當BP=CQ時,四邊形PQCB是平行四邊形
此時![]()
解之得![]()
∴當t=4時,四邊形PQCB是平行四邊形
(3)∵D為線段AB的中點
∴AD=5
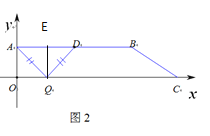
分兩種情況:①若AD為腰時,如圖1:當DA=DQ=5時,△ADQ是等腰三角形
過點D作DE⊥OC
由題意可知D(5,3)
在Rt△DQE中,![]()
∴OQ=5-4=1,即2t=1
∴![]()
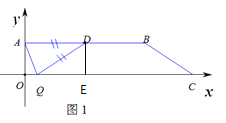
如圖3:當AQ=AD=5時,△ADQ是等腰三角形
在Rt△AOQ中,OQ=![]() 4,即2t=4
4,即2t=4
∴![]()
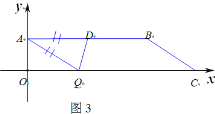
如圖4:當DA=DQ時,△ADQ是等腰三角形
過點D作DE⊥OC
在Rt△DQE中,![]()
∴OQ=5+4=9,即2t=9
∴![]()
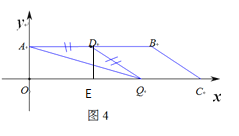
②若AD為底邊,如圖2:當QA=QD時,△ADQ是等腰三角形
過點Q作QE⊥AB,
∵AB∥OC,∠AOC=90°,QE⊥AB
∴∠∠AOC=∠OQE=∠QEA=90°
∴四邊形OQEA是矩形
∴OQ=AE=![]()
即![]() ,
,
∴![]()
綜上:當t為![]() 或2或
或2或![]() 或
或![]() 時,△ADQ是等腰三角形
時,△ADQ是等腰三角形


 應用題點撥系列答案
應用題點撥系列答案 狀元及第系列答案
狀元及第系列答案 同步奧數系列答案
同步奧數系列答案科目:初中數學 來源: 題型:
【題目】如圖,兩個全等的直角三角形重疊在一起,將其中的一個三角形沿著點B到C的方向平移到![]() 的位置,
的位置,![]() ,
,![]() ,平移距離為6,則陰影部分面積為
,平移距離為6,則陰影部分面積為![]()
![]()

A. 24 B. 40 C. 42 D. 48
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某數學興趣小組研究我國古代《算法統宗》里這樣一首詩:我問開店李三公,眾客都來到店中,一房七客多七客,一房九客一房空.詩中后兩句的意思是:如果每一間客房住7人,那么有7人無房可住;如果每一間客房住9人,那么就空出一間房.
(1)求該店有客房多少間?房客多少人?
(2)假設店主李三公將客房進行改造后,房間數大大增加.每間客房收費20錢,且每間客房最多入住4人,一次性定客房18間以上(含18間),房費按8折優惠.若詩中“眾客”再次一起入住,他們如何訂房更合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,請分別根據已知條件進行推理,得出結論,并在括號內注明理由.

①∵ ∠B=∠3(已知),∴______∥______.(______,______)
②∵∠1=∠D (已知),∴______∥______.(______,______)
③∵∠2=∠A (已知),∴______∥______.(______,______)
④∵∠B+∠BCE=180° (已知),∴______∥______.(______,______)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中國最長鐵路隧道西康鐵路秦嶺一線隧道全長十八點四六千米,為目前中國鐵路隧道長度之首,被稱為”神州第一長隧”.為了安全起見在某段隧道兩旁安置了兩座可旋轉探照燈.如圖1所示,燈A發出的光束從AC開始順時針旋轉至AD便立即回轉,燈B發出的光束從BE開始順時針旋轉至BF便立即回轉,兩燈不停交叉照射巡視.若燈A旋轉的速度是每秒3度,燈B旋轉的速度是每秒2度.已知CD∥EF,且∠BAD=![]() ∠BAC,設燈A旋轉的時間為t(單位:秒).
∠BAC,設燈A旋轉的時間為t(單位:秒).
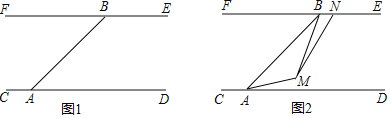
(1)求∠BAD的度數;
(2)若燈B發出的光束先旋轉10秒,燈A發出的光束才開始旋轉,在燈B發出的光束到達BF之前,若兩燈發出的光束互相平行,求燈A旋轉的時間t;
(3)如圖2,若兩燈同時轉動,在燈A發出的光束到達AD之前,若兩燈發出的光束交于點M,過點M作∠AMN交BE于點N,且∠AMN=135°.請探究:∠BAM與∠BMN的數量關系是否發生變化?若不變,請求出其數量關系;若改變,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分別在
分別在![]() 、
、![]() 上,連接
上,連接![]() 、
、![]() 交于點
交于點![]() ,且
,且![]() .
.
(1)如圖1,求證:![]() .
.

(2)如圖2,![]() 是
是![]() 的中點,試探討
的中點,試探討![]() 與
與![]() 的位置關系.
的位置關系.

(3)如圖3,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點,若
的中點,若![]() ,
,![]() ,求
,求![]() 的面積.
的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在平面直角坐標系中,直線y=kx+5與x軸交于點A,與拋物線y=ax2+bx交于B,C兩點,且點B的坐標為(1,7),點C的橫坐標為5.
(1)直接寫出k的值和點C的坐標;
(2)將此拋物線沿對稱軸向下平移n個單位,當拋物線與直線AB只有一個公共點時,求n的值;
(3)在拋物線上有點P,滿足直線AB,AP關于x軸對稱,求點P的坐標..
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 的平分線
的平分線![]() 交
交![]() 于
于![]() ,過
,過![]() 點作與
點作與![]() 垂直的直線
垂直的直線![]() .動點
.動點![]() 從點
從點![]() 出發沿折線
出發沿折線![]() 以每秒1個單位長度的速度向終點
以每秒1個單位長度的速度向終點![]() 運動,運動時間為
運動,運動時間為![]() 秒,同時動點
秒,同時動點![]() 從點
從點![]() 出發沿折線
出發沿折線![]() 以相同的速度運動,當點
以相同的速度運動,當點![]() 到達點
到達點![]() 時
時![]() 、
、![]() 同時停止運動.
同時停止運動.


(1)請寫出![]() 的長為_______,
的長為_______,![]() 的長為_______;
的長為_______;
(2)當![]() 在
在![]() 上
上![]() 在
在![]() 上運動時,如圖(2),設
上運動時,如圖(2),設![]() 與
與![]() 交于點
交于點![]() ,當
,當![]() 為何值時,
為何值時,![]() 為等腰三角形?求出所有滿足條件的
為等腰三角形?求出所有滿足條件的![]() 值.
值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某段河流的兩岸是平行的,數學興趣小組在老師帶領下不用涉水過河就測得河的寬度,他們是這樣做的:
①在河流的一條岸邊B點,選對岸正對的一棵樹A;
②沿河岸直走20m有一樹C,繼續前行20m到達D處;
③從D處沿河岸垂直的方向行走,當到達A樹正好被C樹遮擋住的E處停止行走;
④測得DE的長為5米.
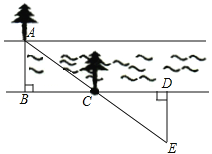
求:(1)河的寬度是多少米?
(2)請你證明他們做法的正確性.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com