
【題目】如圖,已知拋物線y=x2+bx+c的圖象與x軸的一個交點為B(4,0),另一個交點為A,且與y軸交于點C(0,4).
(1)求直線BC與拋物線的解析式;
(2)若點M是拋物線在x軸下方圖象上的一動點,過點M作MN∥y軸交直線BC于點N,當 MN的值最大時,求△BMN的周長.
(3)在(2)的條件下,MN取得最大值時,若點P是拋物線在x軸下方圖象上任意一點,以BC為邊作平行四邊形CBPQ,設平行四邊形CBPQ的面積為S1,△ABN的面積為S2,且S1=4S2,求點P的坐標.

【答案】(1)拋物線的解析式為y=x2﹣5x+4;(2)4+4![]() ;(3)點P的坐標為P(3,﹣2).
;(3)點P的坐標為P(3,﹣2).
【解析】試題(1)利用待定系數法及直線BC上的兩點列方程,從而得出一次函數的解析式;根據二次函數上面的兩點坐標列出兩個方程,從而確定二次函數的一次項系數和常數項;
(2)根據M,N的位置關系,易得他們的橫坐標相同,設出對應的坐標,M(x,x2﹣5x+4)(1<x<4),則N(x,﹣x+4),根據兩點坐標表示出MN的長度為MN=(﹣x+4)﹣(x2﹣5x+4)=﹣x2+4x,然后配方,求出MN的最大值;從而△BMN的周長得解;
(3)先求出△ABN的面積為S2,=3,再根據S1=4S2得S1=12.根據平行四邊形的底邊AB=![]() ,得出平行四邊形的高線BD=
,得出平行四邊形的高線BD=![]() ,再求x粥上面的BE的長度為3,得點E與點A重合,則過點A平行于BC的直線PQ為y=﹣x+1,最后與二次函數聯立方程組,得出點P的坐標.
,再求x粥上面的BE的長度為3,得點E與點A重合,則過點A平行于BC的直線PQ為y=﹣x+1,最后與二次函數聯立方程組,得出點P的坐標.
試題解析:
(1)設直線BC的解析式為y=mx+n,
將B(4,0),C(0,4)兩點的坐標代入,
得,![]() ,
,
∴![]()
所以直線BC的解析式為y=﹣x+4;
將B(4,0),C(0,4)兩點的坐標代入y=x2+bx+c,
得,![]() ,
,
∴![]()
所以拋物線的解析式為y=x2﹣5x+4;
(2)如圖1,
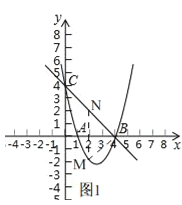
設M(x,x2﹣5x+4)(1<x<4),則N(x,﹣x+4),
∵MN=(﹣x+4)﹣(x2﹣5x+4)=﹣x2+4x=﹣(x﹣2)2+4,
∴當x=2時,MN有最大值4;
∵MN取得最大值時,x=2,
∴﹣x+4=﹣2+4=2,即N(2,2).
x2﹣5x+4=4﹣5×2+4=﹣2,即M(2,﹣2),
∵B(4.0)
可得BN=2![]() ,BM=2
,BM=2![]()
∴△BMN的周長=4+2![]() +2
+2![]() =4+4
=4+4![]()
(3)令y=0,解方程x2﹣5x+4=0,得x=1或4,
∴A(1,0),B(4,0),
∴AB=4﹣1=3,
∴△ABN的面積S2=×3×2=3,
∴平行四邊形CBPQ的面積S1=4S2=12.
如圖2,

設平行四邊形CBPQ的邊BC上的高為BD,則BC⊥BD.
∵BC=4![]() ,
,
∴BCBD=12,
∴BD=![]() .
.
過點D作直線BC的平行線,交拋物線與點P,交x軸于點E,在直線DE上截取PQ=BC,連接CQ,則四邊形CBPQ為平行四邊形.
∵BC⊥BD,∠OBC=45°,
∴∠EBD=45°,
∴△EBD為等腰直角三角形,由勾股定理可得BE=![]() BD=3,
BD=3,
∵B(4,0),
∴E(1,0),
設直線PQ的解析式為y=﹣x+t,
將E(1,0)代入,得﹣1+t=0,解得t=1
∴直線PQ的解析式為y=﹣x+1.
解方程組, ![]() ,
,
得,![]() 或
或![]() ,
,
∵P1(1,0)在x軸上,舍去.
∴點P的坐標為P(3,﹣2).


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:初中數學 來源: 題型:
【題目】已知![]() 中,
中,![]() ,
,![]() 分別平分
分別平分![]() 和
和![]() ,
,![]() 、
、![]() 交于點
交于點![]() .
.

(1)直接寫出![]() 與
與![]() 的數量關系;
的數量關系;
(2)若![]() ,利用(1)的關系,求出
,利用(1)的關系,求出![]() 的度數;
的度數;
(3)利用(2)的結果,試判斷![]() 、
、![]() 、
、![]() 的數量關系,并證明.
的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點O是等邊![]() 內一點
內一點![]() 將
將![]() 繞點C按順時針方向旋轉
繞點C按順時針方向旋轉![]() 得
得![]() ,連接
,連接![]() 已知
已知![]()
![]() .
.
![]() 求證:
求證:![]() 是等邊三角形;
是等邊三角形;
![]() 當
當![]() 時,試判斷
時,試判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
![]() 探究:當
探究:當![]() 為多少度時,
為多少度時,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,點D是BC上一動點,連接AD,將△ACD沿AD折疊,點C落在點C'處,連接C'D交AB于點E,連接BC',當△BC'D是直角三角形時,DE的長為_________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為學生裝一臺直飲水器,課間學生到直飲水器打水.他們先同時打開全部的水籠頭放水,后來又關閉了部分水籠頭.假設前后兩人接水間隔時間忽略不計,且不發生潑灑,直飲水器的余水量![]() (升)與接水時間
(升)與接水時間![]() (分)的函數圖象如圖,請結合圖象回答下列問題:
(分)的函數圖象如圖,請結合圖象回答下列問題:

(1)求當![]() 時,
時,![]() 與
與![]() 之間的函數關系式;
之間的函數關系式;
(2)假定每人水杯接水0.7升,要使40名學生接水完畢,課間10分鐘是否夠用?請計算回答.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算
我區在一項工程招標時,接到甲、乙兩個工程隊的投標書,從投標書中得知:每施工一天,甲工程隊要![]() 萬元,乙工程隊要
萬元,乙工程隊要![]() 萬元,工程小組根據甲、乙兩隊標書的測算,有三種方案:
萬元,工程小組根據甲、乙兩隊標書的測算,有三種方案:![]() 甲隊單獨完成這個工程,剛好如期完成;
甲隊單獨完成這個工程,剛好如期完成;![]() 乙隊單獨完成這個工程要比規定時間多用5天;
乙隊單獨完成這個工程要比規定時間多用5天;![]() **********,剩下的工程由乙隊單獨做,也正好如期完成. 方案
**********,剩下的工程由乙隊單獨做,也正好如期完成. 方案![]() 中“星號”部分被損毀了. 已知,一個同學設規定的工期為
中“星號”部分被損毀了. 已知,一個同學設規定的工期為![]() 天,根據題意列出方程:
天,根據題意列出方程:![]()
(1)請將方案中“星號”部分補充出來________________;
(2)你認為哪個方案節省工程款,請說明你的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,拋物線y=x2+bx+c的對稱軸為直線x=1,拋物線與x軸交于A、B兩點(點A在點B的左側),且AB=4,又P是拋物線上位于第一象限的點,直線AP與y軸交于點D,與對稱軸交于點E,設點P的橫坐標為t.
(1)求點A的坐標和拋物線的表達式;
(2)當AE:EP=1:2時,求點E的坐標;
(3)記拋物線的頂點為M,與y軸的交點為C,當四邊形CDEM是等腰梯形時,求t的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的口袋里裝有分別標有漢字“書”、“ 香”、“ 歷”、“ 城”的四個小球,除漢字不同之外,小球沒有任何區別,每次摸球前先攪拌均勻.
(1)若從中任取一個球,球上的漢字剛好是 “書”的概率為__________.
(2)從中任取一球,不放回,再從中任取一球,請用樹狀圖或列表的方法,求取出的兩個球上的漢字能組成“歷城”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,△ABC是等邊三角形,D是邊BC上的任意一點,∠ADF=60°,且DF交∠ACE的角平分線于點F.


(1)求證:AC=CD+CF;
(2)如圖2,當點D在BC的延長上時,猜想AC、CD、CF的數量關系,并證明你的猜想.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com