
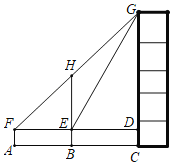
【題目】如圖,某數學興趣小組為測量一顆古樹BH和教學樓CG的高,先在A處用高1.5米的測角儀AF測得古樹頂端H的仰角∠HFE為45°,此時教學樓頂端G恰好在視線FH上,再向前走10米到達B處,又測得教學樓頂端G的仰角∠GED為60°,點A、B、C三點在同一水平線上.求教學樓CG的高.(參考數據:![]() 1.4,
1.4,![]() 1.7)
1.7)
科目:初中數學 來源: 題型:
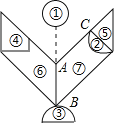
【題目】七巧板是我國古老的益智玩具,受到全世界人的追捧.下圖是由一副“現代智力七巧板經無縫拼接且沒有重疊的軸對稱花朵型圖案,直線AB為對稱軸,其中①②③是直徑為1的圓與半圓,④為直角梯形,⑤為等腰直角三角形,⑥⑦是有一組對邊平行且銳角皆為45°的拼板.若已知④的周長是AB的3倍,⑥的周長是AB的5倍,則圖中線段AC的長度為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
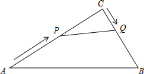
【題目】如圖,在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,現有動點P從點A出發,沿AC向點C方向運動,動點Q從點C出發,沿CB向點B方向運動,如果點P的速度是4cm/秒,點Q的速度是2cm/秒,它們同時出發,當有一點到達所在線段的端點時,就停止運動.設運動時間為t秒.求:
(1)當t=3秒時,這時,P,Q兩點之間的距離是多少?
(2)若△CPQ的面積為S,求S關于t的函數關系式.
(3)當t為多少秒時,以點C,P,Q為頂點的三角形與△ABC相似?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸相交于
軸相交于![]() 兩點(點
兩點(點![]() 位于點
位于點![]() 的左側),與
的左側),與![]() 軸相交于點
軸相交于點![]() ,
,![]() 是拋物線的頂點,直線
是拋物線的頂點,直線![]() 是拋物線的對稱軸,且點
是拋物線的對稱軸,且點![]() 的坐標為
的坐標為![]() .
.
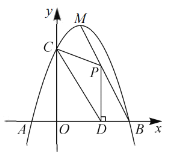
(1)求拋物線的解析式.
(2)已知![]() 為線段
為線段![]() 上一個動點,過點
上一個動點,過點![]() 作
作![]() 軸于點
軸于點![]() .若
.若![]() 的面積為
的面積為![]() .
.
①求![]() 與
與![]() 之間的函數關系式,并寫出自變量
之間的函數關系式,并寫出自變量![]() 的取值范圍;
的取值范圍;
②當![]() 取得最值時,求點
取得最值時,求點![]() 的坐標.
的坐標.
(3)在(2)的條件下,在線段![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 為等腰三角形?如果存在,請求出點
為等腰三角形?如果存在,請求出點![]() 的坐標;如果不存在,請說明理由.
的坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,二次函數拋物線![]() 過點
過點![]() 和
和![]() ,對稱軸為直線
,對稱軸為直線![]() .
.
(1)求二次函數的表達式和頂點![]() 的坐標.
的坐標.
(2)將拋物線在坐標平面內平移,使其過原點,若在平移后,第二象限的拋物線上存在點![]() ,使
,使![]() 為等腰直角三角形,請求出拋物線平移后的表達式,并指出其中一種情況的平移方式.
為等腰直角三角形,請求出拋物線平移后的表達式,并指出其中一種情況的平移方式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中央電視臺的“中國詩詞大賽”節目文化品位高,內容豐富,某校初二年級模擬開展“中國詩詞大賽”比賽,對全年級同學成績進行統計后分為“優秀”、“良好”、“一般”、“較差”四個等級,并根據成績繪制成如下兩幅不完整的統計圖,請結合統計圖中的信息,回答下列問題:

(1)扇形統計圖中“優秀”所對應的扇形的圓心角為 度,并將條形統計圖補充完整.
(2)此次比賽有四名同學活動滿分,分別是甲、乙、丙、丁,現從這四名同學中挑選兩名同學參加學校舉行的“中國詩詞大賽”比賽,請用列表法或畫樹狀圖法,求出選中的兩名同學恰好是甲、丁的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形紙片ABCD中,EF∥AB,M,N是線段EF的兩個動點,且MN=![]() EF,若把該正方形紙片卷成一個圓柱,使點A與點B重合,若底面圓的直徑為6cm,則正方形紙片上M,N兩點間的距離是____________cm.
EF,若把該正方形紙片卷成一個圓柱,使點A與點B重合,若底面圓的直徑為6cm,則正方形紙片上M,N兩點間的距離是____________cm.

查看答案和解析>>
科目:初中數學 來源: 題型:
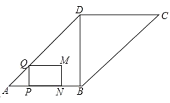
【題目】如圖,在ABCD中,∠ABD=90°,AD= 5,BD=3,點P從點A出發,沿折線AB- BC以每秒個單位長度的速度向終點C運動(點P不與點A、B、C重合).在點P運動的過程中,過點P作AB所在直線的垂線.交邊AD或邊CD于點Q,以PQ為一邊作矩形PQMN,且QM=2.MN與BD在PQ的同側,設點P的運動時間為t(秒),
(1)當t= 5時,求線段CP的長;
(2)求線段PQ的長(用含t的代數式表示);
(3)當點M落在BD上時,求t的值;
(4)當矩形PQMN與ABCD重疊部分圓形為五邊形時,直接寫出t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點P是平面直角坐標系中的一點且不在坐標軸上,過點P向x軸、y軸作垂線段,若垂線段的長度的和為4,則點P叫做“垂距點”,例如:如圖中的點P(1,3)是“垂距點”.
(1)在點A(﹣2,2),![]() ,C(﹣1,5)是“垂距點”是 ;
,C(﹣1,5)是“垂距點”是 ;
(2)若![]() 是“垂距點”,求m的值.
是“垂距點”,求m的值.
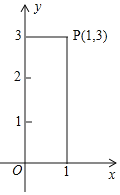
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com