
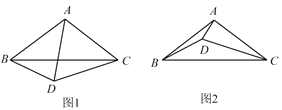
【題目】在![]() 中,
中,![]() ,
,![]() .將線段
.將線段![]() 繞著點
繞著點![]() 逆時針旋轉得到線段
逆時針旋轉得到線段![]() ,旋轉角為
,旋轉角為![]() ,且
,且![]() ,連接
,連接![]() 、
、![]() .
.
(1)如圖 1,當![]() 時,
時,![]() 的大小為 ;
的大小為 ;
(2)如圖 2,當![]() 時,
時,![]() 的大小為 ;
的大小為 ;
(提示:可以作點D關于直線BC的對稱點)
(3)當![]() 為 ° 時,可使得
為 ° 時,可使得![]() 的大小與(1)中
的大小與(1)中![]() 的結果相等.
的結果相等.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,或
,或![]() ,
,![]() .
.
【解析】
(1)由∠BAC=100,AB=AC,可以確定∠ABC=∠ACB=40,旋轉角為α,α=60°時△ACD是等邊三角形,且AC=AD=AB=CD,知道∠BAD的度數,進而求得∠CBD的大小;
(2) 作點D關于直線BC的對稱點D/,連接A D/、B D/、C D/,根據旋轉和對稱的性質即可得;
(3)結合(1)(2)的解題過程可以發現規律,△ACD是等邊三角形時,CD在△ABC內部時,CD在△ABC外部時,求得答案.
解:(1)∵∠BAC=100,AB=AC,
∴∠ABC=∠ACB=40,當α=60時,
由旋轉的性質得AC=CD,
∴△ACD是等邊三角形,
∴∠DAC=60,
∴∠BAD=∠BAC∠DAC=10060=40,
∵AB=AC,AD=AC,
∴AB=AD,
∴∠ABD=∠ADB=![]() (180∠BAD)=70,
(180∠BAD)=70,
∴∠CBD=∠ABD∠ABC=7040=30;
(2)如圖,作點D關于直線BC的對稱點D/,連接A D/、B D/、C D/,
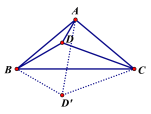
∵∠BAC=100,AB=AC,
∴∠ABC=∠ACB=40,當α=20時,
∴∠BCD=20,
由旋轉和對稱的性質可知,∠BCD/=∠BCD=20,AC=CD=CD/,
∴△ACD/是等邊三角形,
由(1)可知∠CBD/=30,
∴∠CBD=∠CBD/=30;
(3)①由(1)可知,∠α=60時可得∠CBD=30;
②由(2)可知,∠α=20時可得∠CBD=30;
③在圖1中以C為圓心CD為半徑畫圓弧交BD的延長線于點D1,連接CD1,
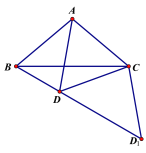
∵∠CDD1=∠CBD+∠BCD=30+![]() =50,
=50,
∴∠DCD1=1802∠CDD1=180100=80,
∴∠α=60+∠DCD1=140;
④在圖2中以C為圓心CD為半徑畫圓弧交BD的延長線于點D2,連接CD2,
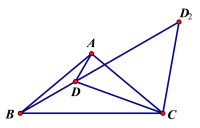
∵∠CDD2=∠CBD+∠BCD=30+![]() =50,
=50,
∴∠DCD2=1802∠CDD2=180100=80,
∴∠ACD2=∠DCD2-∠ACD=80-20=60,
∴∠α=360-60=300.
綜上所述,α為20、60、140、300時,∠CBD=30.
故答案為:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,或
,或![]() ,
,![]() .
.


科目:初中數學 來源: 題型:
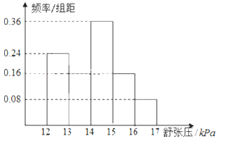
【題目】為了研究某藥品的療效,現選取若干名志愿者進行臨床試驗.所有志愿者的舒張壓數據(單位:kPa)的分組區間為[12,13),[13,14),[14,15),[15,16),[16,17],將其按從左到右的順序分別編號為第一組、第二組、…、第五組.如圖是根據試驗數據制成的頻率分布直方圖.
(1)若第一組接受治療的志愿者有12人,則第三組接受治療的志愿者有多少人?
(2)若接受治療的志愿者共有50人,規定舒張壓在14kpa以上的志愿者接受進一步的臨床試驗,若從三組志愿者中按比例分配20張床位,則舒張壓數據在[14,15)的志愿者總共可以得到多少張床位?
查看答案和解析>>
科目:初中數學 來源: 題型:
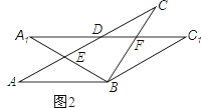
【題目】在△ABC中,AB=BC=2,∠ABC=120°,將△ABC繞點B順時針旋轉角α(0°<α<90°)得△A1BC1,A1B交AC于點E,A1C1分別交AC、BC于D、F兩點.
(1)如圖1,觀察并猜想,在旋轉過程中,線段BE與BF有怎樣的數量關系?并證明你的結論;
(2)如圖2,當α=30°時,試判斷四邊形BC1DA的形狀,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀新知:化簡后,一般形式為ax4+bx2+c=0(a≠0)的方程,由于其具有只含有未知數偶次項的四次方程,我們稱其為“雙二次方程”.這類方程我們一般可以通過換元法求解.如:求解2x4-5x2+3=0的解.
解:設![]() ,則原方程可化為:
,則原方程可化為:![]() ,解之得
,解之得![]()
當![]() 時,
時,![]() , ∴
, ∴![]() ;
;
當![]() 時
時 ![]() ∴
∴![]() .
.
綜上,原方程的解為:![]() ,
,![]() .
.
(1)通過上述閱讀,請你求出方程![]() 的解;
的解;
(2)判斷雙二次方程ax4+bx2+c=0(a≠0)根的情況,下列說法正確的是 (選出正確的答案).
①當b2-4ac≥0時,原方程一定有實數根;
②當b2-4ac<0時,原方程一定沒有實數根;
③原方程無實數根時,一定有b2-4ac<0.
查看答案和解析>>
科目:初中數學 來源: 題型:
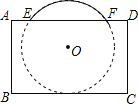
【題目】把球放在長方體紙盒內,球的一部分露出盒外,其主視圖如圖.⊙O與矩形ABCD的邊BC,AD分別相切和相交(E,F是交點),已知EF=CD=8,則⊙O的半徑為
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,利用一面墻(墻的長度不超過45m),用80m長的籬笆圍一個矩形場地.
(1)怎樣圍才能使矩形場地的面積為750m2?
(2)能否使所圍矩形場地的面積為810m2 ,為什么?

查看答案和解析>>
科目:初中數學 來源: 題型:
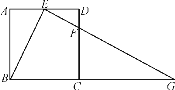
【題目】如圖,在正方形ABCD中,E、F分別是邊AD、CD上的點,AE=ED,DF=![]() DC,連接EF并延長交BC的延長線于點G.
DC,連接EF并延長交BC的延長線于點G.
(1)求證:△ABE∽△DEF;
(2)若正方形的邊長為4,求BG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
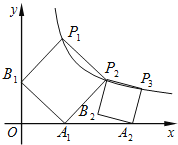
【題目】正方形的A1B1P1P2頂點P1、P2在反比例函數y=![]() (x>0)的圖象上,頂點A1、B1分別在x軸、y軸的正半軸上,再在其右側作正方形P2P3A2B2,頂點P3在反比例函數y=
(x>0)的圖象上,頂點A1、B1分別在x軸、y軸的正半軸上,再在其右側作正方形P2P3A2B2,頂點P3在反比例函數y=![]() (x>0)的圖象上,頂點A2在x軸的正半軸上,則點P3的坐標為 .
(x>0)的圖象上,頂點A2在x軸的正半軸上,則點P3的坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
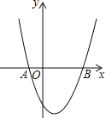
【題目】如圖,已知拋物線y=x2+bx+c經過A(﹣1,0)、B(3,0)兩點.
(1)求拋物線的解析式和頂點坐標;
(2)點P為拋物線上一點,若S△PAB=10,求出此時點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com