
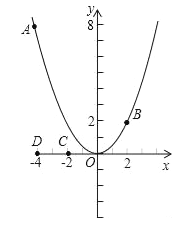
【題目】如圖,已知點A(﹣4,8)和點B(2,n)在拋物線y=ax2上.
(1)求a的值及點B關于x軸對稱點P的坐標,并在x軸上找一點Q,使得AQ+QB最短,求出點Q的坐標;
(2)平移拋物線y=ax2,記平移后點A的對應點為A′,點B的對應點為B′,點C(﹣2,0)和點D(﹣4,0)是x軸上的兩個定點.
①當拋物線向左平移到某個位置時,A′C+CB′最短,求此時拋物線的函數解析式;
②當拋物線向左或向右平移時,是否存在某個位置,使四邊形A′B′CD的周長最短?若存在,求出此時拋物線的函數解析式;若不存在,請說明理由.
【答案】(1)a= ![]() ,P的坐標為(2,﹣2),Q的坐標是(
,P的坐標為(2,﹣2),Q的坐標是(![]() ,0);(2)①
,0);(2)①![]() ;②存在,
;②存在,![]() .
.
【解析】試題分析:(1)把(﹣4,8)代入y=ax2可求得a的值,把x=2代入所求的拋物線解析式,可得n的值,那么P的坐標為2,縱坐標為﹣n,求得AP與x軸的交點即為Q的坐標;
(2)A′C+CB′最短,說明拋物線向左平移了線段CQ的距離,用頂點式設出相應的函數解析式,把新頂點坐標代入即可;
(3)左右平移時,使A′D+DB′′最短即可,那么作出點A′關于x軸對稱點的坐標為A′′,得到直線A′′B′′的解析式,讓y=0,求得相應的點的坐標;進而得到拋物線頂點平移的規律,用頂點式設出相應的函數解析式,把新頂點坐標代入即可.
試題解析:解:(1)將點A(﹣4,8)的坐標代入y=ax2,解得a=![]() ;
;
將點B(2,n)的坐標代入y=![]() x2,求得點B的坐標為(2,2),則點B關于x軸對稱點P的坐標為(2,﹣2),設直線AP的解析式為y=kx+b,
x2,求得點B的坐標為(2,2),則點B關于x軸對稱點P的坐標為(2,﹣2),設直線AP的解析式為y=kx+b,![]() ,解得:
,解得: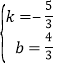 ,∴直線AP的解析式是y=﹣
,∴直線AP的解析式是y=﹣![]() x+
x+![]() ,令y=0,得:x=
,令y=0,得:x=![]() .
.
即所求點Q的坐標是(![]() ,0);
,0);
(2)①CQ=|﹣2﹣![]() |=
|=![]() ,
,
故將拋物線y=![]() x2向左平移
x2向左平移![]() 個單位時,A′C+CB′最短,
個單位時,A′C+CB′最短,
此時拋物線的函數解析式為y=![]() (x+
(x+![]() )2;
)2;
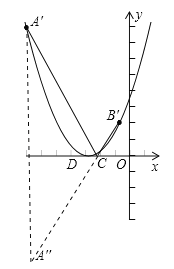
②左右平移拋物線y=![]() x2.∵線段A′B′和CD的長是定值,∴要使四邊形A′B′CD的周長最短,只要使A′D+CB′最短;
x2.∵線段A′B′和CD的長是定值,∴要使四邊形A′B′CD的周長最短,只要使A′D+CB′最短;
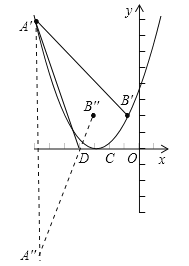
第一種情況:如果將拋物線向右平移,顯然有A′D+CB′>AD+CB,∴不存在某個位置,使四邊形A′B′CD的周長最短;
第二種情況:設拋物線向左平移了b個單位,則點A′和點B′的坐標分別為A′(﹣4﹣b,8)和B′(2﹣b,2).∵CD=2,∴將點B′向左平移2個單位得B′′(﹣b,2),要使A′D+CB′最短,只要使A′D+DB′′最短,點A′關于x軸對稱點的坐標為A′′(﹣4﹣b,﹣8).∵直線A′′B′′的解析式為y=![]() x+
x+![]() b+2.要使A′D+DB′′最短,點D應在直線A′′B′′上,將點D(﹣4,0)代入直線A′′B′′的解析式,解得:b=
b+2.要使A′D+DB′′最短,點D應在直線A′′B′′上,將點D(﹣4,0)代入直線A′′B′′的解析式,解得:b=![]() ,∴將拋物線向左平移時,存在某個位置,使四邊形A′B′CD的周長最短,此時拋物線的函數解析式為y=
,∴將拋物線向左平移時,存在某個位置,使四邊形A′B′CD的周長最短,此時拋物線的函數解析式為y=![]() (x+
(x+![]() )2.
)2.


科目:初中數學 來源: 題型:
【題目】定義:數學活動課上,陳老師給出如下定義:有一組對邊相等而另一組對邊不相等的凸四邊形叫做對等四邊形.
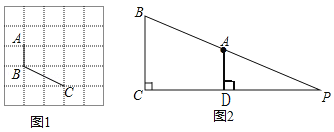
理解:(1)如圖1,已知A、B、C在格點(小正方形的頂點)上,請在方格圖中畫出以格點為頂點,AB、BC為邊的兩個對等四邊形ABCD;
應用:(2)如圖2,在Rt△PBC中,∠PCB=90°,BC=9,點A在BP邊上,且AB=13.AD⊥PC,CD=12,若PC上存在符合條件的點M,使四邊形ABCM為對等四邊形,求出CM的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在數軸上A點表示數a,B點示數b,C點表示數c,b是最小的正整數,且a,b滿足![]() +(c-7)2=0.
+(c-7)2=0.
(1) a= ,b= ,c= .
(2) 若將數軸折疊,使得A點與C點重合,則點B與數 表示的點重合.
(3) 點A,B,C開始在數軸上運動,若點A以每秒1個單位長度的速度向左運動,同時,點B和點C分別以每秒2個單位長度和4個單位長度的速度向右運動,假設t秒鐘過后,若點A與點B之間的距離表示為AB,點A與點C之間的距離表示為AC,點B與點C之間的距離表示為BC.則AB= ,AC= ,BC= .(用含t的代數式表示)
(4) 請問:3BC-2AB的值是否隨著時間t的變化而改變? 若變化,請說明理由;若不變,請求其值.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y= ![]() x+6的圖象與x軸、y軸分別交于A、B兩點,點C與點A關于y軸對稱.動點P、Q分別在線段AC、AB上(點P與點A、C不重合),且滿足∠BPQ=∠BAO。
x+6的圖象與x軸、y軸分別交于A、B兩點,點C與點A關于y軸對稱.動點P、Q分別在線段AC、AB上(點P與點A、C不重合),且滿足∠BPQ=∠BAO。
(1)求點A、 B的坐標及線段BC的長度;
(2)當點P在什么位置時,△APQ≌△CBP,說明理由;
(3)當△PQB為等腰三角形時,求點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司準備投資開發A、B兩種新產品,通過市場調研發現:如果單獨投資A種產品,則所獲利潤yA(萬元)與投資金額x(萬元)之間滿足正比例函數關系:yA=kx;如果單獨投資B種產品,則所獲利潤yB(萬元)與投資金額x(萬元)之間滿足二次函數關系:yB=ax2+bx.根據公司信息部的報告,yA、yB(萬元)與投資金額x(萬元)的部分對應值(如下表)

(1)求正比例函數和二次函數的解析式;
(2)如果公司準備投資20萬元同時開發A、B兩種新產品,請你設計一個能獲得最大利潤的投資方案,并求出按此方案能獲得的最大利潤是多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,兩個邊長分別為a,b(a>b)的正方形連在一起,三點C,B,F在同一直線上,反比例函數y=![]() 在第一象限的圖象經過小正方形右下頂點E.若OB2﹣BE2=10,則k的值是( )
在第一象限的圖象經過小正方形右下頂點E.若OB2﹣BE2=10,則k的值是( )

A. 3 B. 4 C. 5 D. 4![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,對角線AC,BD交于點O,E,F分別是邊BC,AD的中點,AB=2,BC=4,一動點P從點B出發,沿著B﹣A﹣D﹣C在矩形的邊上運動,運動到點C停止,點M為圖1中某一定點,設點P運動的路程為x,△BPM的面積為y,表示y與x的函數關系的圖象大致如圖2所示.則點M的位置可能是圖1中的( )
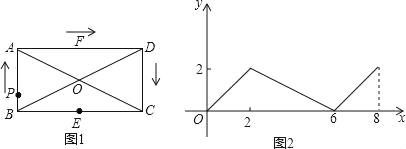
A. 點CB. 點OC. 點ED. 點F
查看答案和解析>>
科目:初中數學 來源: 題型:
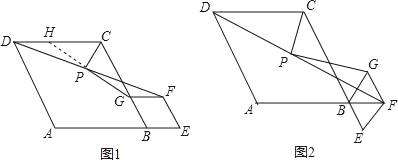
【題目】閱讀下列材料:問題:如圖1,在菱形ABCD和菱形BEFG中,∠ABC=∠BEF=60°,點A,B,E在同一條直線上,P是線段DF的中點,連接PG,PC,探究PG與PC的位置關系
小穎同學的思路是:延長GP交DC于點H,構造全等三角形,經過推理使問題得到解決.
請你參考小穎同學的思路,探究并解決下列問題:
(1)請你寫出上面問題中線段PG與PC的位置關系;
(2)將圖1中的菱形BEFG繞點B順時針旋轉,使菱形BEFG的對角線BF恰好與菱形ABCD的邊AB在同一條直線上,原問題申的其他條件不變(如圖2).你在(1)中得到的結論是否發生變化?寫出你的猜想并加以證明,
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】做大小兩個長方體紙盒,尺寸如下(單位:cm)
長 | 寬 | 高 | |
小紙盒 |
|
|
|
大紙盒 |
|
|
|
(1)做這兩個紙盒共用料多少平方厘米?
(2)做大紙盒比做小紙盒多用料多少平方厘米?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com