
【題目】如圖,在平面直角坐標系中,直線![]() 與y軸交于點C(0,6),與x軸交于點B.
與y軸交于點C(0,6),與x軸交于點B.
(1)求這條直線的解析式;(2)直線AD與(1)中所求的直線相交于點D(![]() ,n),點A的坐標為(
,n),點A的坐標為(![]() ).
).

①求n的值及直線AD的解析式;
②求△ABD的面積.
【答案】(1)![]() ;(2)①n=8,y=4x+12;②24.
;(2)①n=8,y=4x+12;②24.
【解析】分析:(1)將點C(0,6)代入y=-2x+a求得a的值即可;(2)①將點D坐標代入直線BD解析式可得n的值,再利用待定系數法可求得直線AD解析式;②令直線BC的解析式中y=0求出x值,由此即可得出點B的坐標,再由點A、D的坐標,利用三角形的面積公式即可得出結論;
本題解析:
(1)∵直線![]() 與y軸交于點C(0,6),
與y軸交于點C(0,6),
∴a=6,
∴該直線解析式為![]() .
.
(2)①∵點D(![]() ,n)在直線BC上,
,n)在直線BC上,
∴n=![]() ×(
×(![]() )+6=8,
)+6=8,
∴點D(![]() ,8).
,8).
設直線AD的解析式為y=kx+b,
將點A(![]() ,0)、D(
,0)、D(![]() ,8)代入y=kx+b中,
,8)代入y=kx+b中,
得: ![]() ,解得:
,解得: ![]() ,
,
∴直線AD的解析式為y=4x+12.
②令![]() 中y=0,則
中y=0,則![]() ,解得:x=3,
,解得:x=3,
∴點B(3,0).
∵A(![]() ,0)、D(
,0)、D(![]() ,8),
,8),
∴AB=6.
S△ABD=![]() .
.


科目:初中數學 來源: 題型:
【題目】(2016山西省第22題)綜合與實踐
問題情境
在綜合與實踐課上,老師讓同學們以“菱形紙片的剪拼”為主題開展數學活動,如圖1,將一張菱形紙片ABCD(![]() )沿對角線AC剪開,得到
)沿對角線AC剪開,得到![]() 和
和![]() .
.
操作發現
(1)將圖1中的![]() 以A為旋轉中心,逆時針方向旋轉角
以A為旋轉中心,逆時針方向旋轉角![]() ,使
,使 ![]() ,得到如圖2所示的
,得到如圖2所示的![]() ,分別延長BC 和
,分別延長BC 和![]() 交于點E,則四邊形
交于點E,則四邊形![]() 的狀是 ;
的狀是 ;
(2)創新小組將圖1中的![]() 以A為旋轉中心,按逆時針方向旋轉角
以A為旋轉中心,按逆時針方向旋轉角![]() ,使
,使![]() ,得到如圖3所
,得到如圖3所
示的![]() ,連接DB,
,連接DB,![]() ,得到四邊形
,得到四邊形![]() ,發現它是矩形.請你證明這個論;
,發現它是矩形.請你證明這個論;
(3)縝密小組在創新小組發現結論的基礎上,量得圖3中BC=13cm,AC=10cm,然后提出一個問題:將![]() 沿著射線DB方向平移acm,得到
沿著射線DB方向平移acm,得到![]() ,連接
,連接![]() ,
,![]() ,使四邊形
,使四邊形![]() 恰好為正方形,求a的值.請你解答此問題;
恰好為正方形,求a的值.請你解答此問題;
(4)請你參照以上操作,將圖1中的![]() 在同一平面內進行一次平移,得到
在同一平面內進行一次平移,得到![]() ,在圖4中畫出平移后構造出的新圖形,標明字母,說明平移及構圖方法,寫出你發現的結論,不必證明.
,在圖4中畫出平移后構造出的新圖形,標明字母,說明平移及構圖方法,寫出你發現的結論,不必證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地的一座人行天橋如圖所示,天橋高為6米,坡面BC的坡度為1:1,為了方便行人推車過天橋,有關部門決定降低坡度,使新坡面的坡度為1:![]() .
.
(1)求新坡面的坡角a;
(2)原天橋底部正前方8米處(PB的長)的文化墻PM是否需要拆橋?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了加強學生的安全意識,某校組織了學生參加安全知識競賽,從中抽取了部分學生成績(得分數取正
整數,滿分為![]() 分)進行統計,已知
分)進行統計,已知![]() 組的頻數
組的頻數![]() 比
比![]() 組的頻數
組的頻數![]() 小,繪制統計頻數分別直方圖(未完成)
小,繪制統計頻數分別直方圖(未完成)
和扇形統計圖如下,
請解答下列問題:
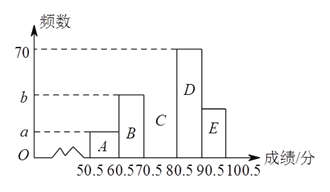
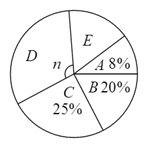
(![]() )樣本容量為:__________,
)樣本容量為:__________, ![]() 為__________.
為__________.
(![]() )
)![]() 為__________,
為__________, ![]() 組所占比例為__________
組所占比例為__________![]() .
.
(![]() )補全頻數分布直方圖.
)補全頻數分布直方圖.
(![]() )若成績在
)若成績在![]() 分以上記作優秀,全校共有
分以上記作優秀,全校共有![]() 名學生,估計成績優秀學生有__________名.
名學生,估計成績優秀學生有__________名.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算機中常用的十六進制是逢16進1的計數制,采用數字0~9和字母A~F共16個計數符號,這些符號與十進制的數的對應關系如下表:
十六進制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
十進制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
例如,用十六進制表示:C+F=1B,19﹣F=A,18÷4=6,則A×B=( )
A. 72 B. 6E C. 5F D. B0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com