
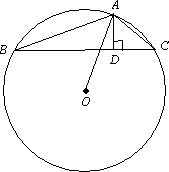
在鈍角△ABC中,AD⊥BC,垂足為D點,且AD與DC的長度為x2-7x+12=0方程的兩個根,⊙O是△ABC的外接圓,如果BD長為a(a>0).
求△ABC的外接圓⊙O的面積.
|
解:∵AD與DC的長度為x2-7x+12的兩根 ∴有兩種情況:①AD=3,DC=4 ②AD=4,DC=3 由勾股定理:求得AC=5 (求△ABC的外接圓⊙O的直徑長,介紹三種方法供參考) 方法一:連接AO并延長交⊙O于E點,連接BE ∴∠ABE=90° 又∵∠E=∠C ∴△ABE∽△ADC,∴ 方法二:連接AO并延長交⊙O于E點,連接BE ∴∠ABE=90° 在Rt△ADC中:sinC= 又∵∠C=∠E,∴sinC=sinE ∴ 方法三:在Rt△ADC中,sinC= 由正弦定理: 可得: 當AD=3,DC=4時, ⊙O的面積為: 當AD=4,DC=3時, ⊙O的面積為: |
|
結果有兩種情況,只求出一種正確結果,只能得8分 |


 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:初中數學 來源: 題型:
 26、如圖,在鈍角△ABC中,點D、E分別是邊AC、BC的中點,且DA=DE.有下列結論:①∠1=∠2;②∠1=∠3;③∠B=∠C;④∠B=∠3.其中一定正確的結論有( )個.
26、如圖,在鈍角△ABC中,點D、E分別是邊AC、BC的中點,且DA=DE.有下列結論:①∠1=∠2;②∠1=∠3;③∠B=∠C;④∠B=∠3.其中一定正確的結論有( )個.查看答案和解析>>
科目:初中數學 來源: 題型:
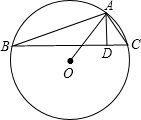 在鈍角△ABC中,AD⊥BC,垂足為D點,且AD與DC的長度為x2-7x+12=0方程的兩個根,⊙O是△ABC的外接圓,如果BD長為a(a>0).求△ABC的外接圓⊙O的面積.
在鈍角△ABC中,AD⊥BC,垂足為D點,且AD與DC的長度為x2-7x+12=0方程的兩個根,⊙O是△ABC的外接圓,如果BD長為a(a>0).求△ABC的外接圓⊙O的面積.查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com