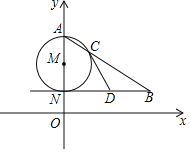
【題目】如圖，AN是⊙M的直徑，NB∥x軸，AB交⊙M于點C．
（1）若點A（0，6），N（0，2），∠ABN=30°，求點B的坐標；
（2）若D為線段NB的中點，求證：直線CD是⊙M的切線．
【答案】(1) B（
，2）．(2)證明見解析.
【解析】
試題分析：（1）在Rt△ABN中，求出AN、AB即可解決問題；
（2）連接MC，NC．只要證明∠MCD=90°即可
試題解析：（1）∵A的坐標為（0，6），N（0，2），
∴AN=4，
∵∠ABN=30°，∠ANB=90°，
∴AB=2AN=8，
∴由勾股定理可知：NB=
，
∴B（，2）．
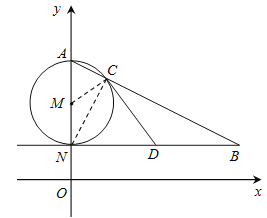
（2）連接MC，NC
∵AN是⊙M的直徑，
∴∠ACN=90°，
∴∠NCB=90°，
在Rt△NCB中，D為NB的中點，
∴CD=
NB=ND，
∴∠CND=∠NCD，
∵MC=MN，
∴∠MCN=∠MNC，
∵∠MNC+∠CND=90°，
∴∠MCN+∠NCD=90°，
即MC⊥CD．
∴直線CD是⊙M的切線．
同步練習強化拓展系列答案科目：初中數學 來源： 題型：
【題目】在△ABC中,BC=10,AB的垂直平分線與AC的垂直平分線分別交BC于點D、E,且DE=4,則AD+AE的長度為________________
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，一次函數y=kx+b的圖象分別交x軸、y軸于A、B兩點，與反比例函數 
的圖象交于C、D兩點，DE⊥x軸于點E．已知C點的坐標是（6，﹣1），DE=3．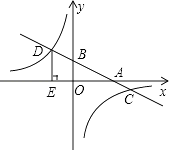 
（1）求反比例函數與一次函數的解析式．
（2）根據圖象直接回答：當x為何值時，一次函數的值大于反比例函數的值？
查看答案和解析>>
科目：初中數學 來源： 題型：
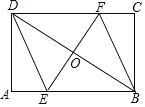
【題目】如圖，矩形ABCD中，AB=6，BC=4，過對角線BD中點O的直線分別交AB，CD邊于點E，F．
（1）求證：四邊形BEDF是平行四邊形；
（2）當四邊形BEDF是菱形時，求EF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD中，∠A=∠ABC=90°，AD=3，BC=5，E是邊CD的中點，連結BE并延長與AD的延長線相交于點F．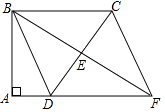 
（1）求證：四邊形BDFC是平行四邊形．
（2）若BD=BC，求四邊形BDFC的面積．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com