解答: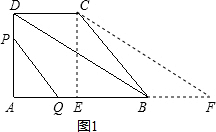
解:(1)如圖1,過C點作CE⊥AB,
∵直角梯形ABCD中,AB∥CD,∠A=90°,
∴四邊形ADCE是矩形,
∴AD=CE,AE=CD,
∵AB=6,AD=4,DC=3,
∴AD=CE=4,AE=CD=3,EB=AB-AE=3,
∴BC=
=5,
∴點P到達終點B時,所走的路程為AD+CD+BC=4+3+5=12,
∵點P從點A出發沿折線段AD-DC-CB以每秒3個單位長的速度向點B勻速運動,
∴當點P到達終點B時,t=
=4.
答:t的值為4;
(2)當點P運動到AD時上時,
∵△APQ為直角三角形,△APQ的面積為S,
∴s=
PA•AQ,
∵點P從點A出發沿折線段AD-DC-CB以每秒3個單位長的速度向點B勻速運動,
點Q從點A出發沿射線AB方向以每秒2個單位長的速度勻速運動,
∴s=
×3t×2t=3t
2.
當點P運動到DC時上時,
s=
×AD×2t=
×4×2t=4t,
答:點P運動到AD上時,S與t的函數關系式為s=3t
2;
當點P運動到DC時上時,S與t的函數關系式為s=4t,
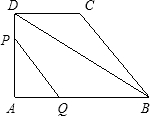
(3)若PQ∥DB,則點P、Q必在DB同側.
①當點Q在AB上,點P在AD上時,
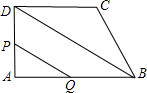
∵AP:AQ=3t:2t=3:2,
而AD:AB=4:6=2:3,
∴AP:AQ≠AD:AB,則此情景下PQ不平行DB;
②因點Q沿射線AB運動,
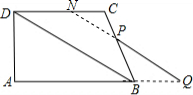
所以點Q在AB延長線上,點P在CB上時,即當3<t<4 時,PB=12-3t,PC=3t-7,BQ=2t-6.
若PQ∥DB,設直線PQ交DC與N,
∵DC∥AB,
∴△PCN∽△PBQ,
∴CN:BQ=PC:PB,則CN=
;
又∵NQ∥DB,
∴CN:CD=CP:CB,
則CN=
,
所以
=
,
解得t=
(符合題意).
綜上情景①、②所述,當t=
時,PQ∥DB.
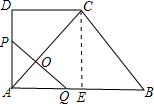
(4)存在t=3
,使PQ⊥AC.理由如下:
分四種情況討論:
①當0<t≤
時,P在AD上,Q在AE上,設PQ與AC交于點O;
如圖,若PQ⊥AC,則△AOP∽△ADC,∴AP:AC=AO:AD,∴3t:5=AO:4,∴AO=
t,
又若PQ⊥AC,則△QOA∽△ADC,∴OA:DC=AQ:AC,∴AO:3=2t:5,∴AO=
t,
∴
t=
t,∴t=0,此解不符合題意,則此時PQ⊥AC不成立;
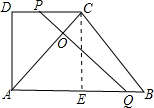
②當
<t≤
時,P在DC上,Q在AB上,設PQ與AC交于點O;
如圖,若PQ⊥AC,則△COP∽△CDA,∴CP:AC=OC:CD,∴(7-3t):5=OC:3,∴OC=
(7-3t),
又若PQ⊥AC,則△QOA∽△ADC,∴OA:DC=AQ:AC,∴AO:3=2t:5,∴AO=
t,
∵OC+OA=AC,∴
(7-3t)+
t=5,∴t=-
,此解不符合題意,則此時PQ⊥AC不成立;
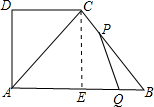
③當
<t≤3時,P在CB上,Q在AB上;
如圖,顯然此時PQ不可能與AC垂直;
④當3<t≤4時,P在CB上,Q在AB的延長線上,設直線PQ與AC交于點O,過點P作PM⊥AB于M.
在△BPM中,PM=BP•sin∠PBM=
BP=
(12-3t),MQ=
.
由△QAO∽△ACD,得AO:AQ=CD:AC=3:5.
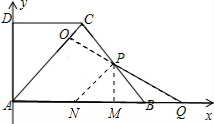
過點P作PN⊥OQ交AB于N.則PN=BP=12-3t,BN=2BM=
BP,
NQ=BN+BQ=
BP+(2t-6)=
.
由△QOA∽△QPN,得AO:AQ=PN:NQ,
即3:5=BP:
,
∴25BP=18BP+30t-90,
∴7BP=7(12-3t)=30t-90,
∴51t=174,
解得t=3
=3
,
綜上可知,當t=3
時,PQ⊥AC.

 運動,點Q也隨之停止,設點P,Q的運動時間是t秒(t>0).
運動,點Q也隨之停止,設點P,Q的運動時間是t秒(t>0). 解:(1)如圖1,過C點作CE⊥AB,
解:(1)如圖1,過C點作CE⊥AB,

 (4)存在t=3
(4)存在t=3 ②當
②當 ③當
③當 過點P作PN⊥OQ交AB于N.則PN=BP=12-3t,BN=2BM=
過點P作PN⊥OQ交AB于N.則PN=BP=12-3t,BN=2BM=

 名校課堂系列答案
名校課堂系列答案 如圖,直角梯形ABCD中,AD∥BC,∠ABC=90°,點E是AB邊上一點,AE=BC,DE⊥EC,取DC的中點F,連接AF、BF.
如圖,直角梯形ABCD中,AD∥BC,∠ABC=90°,點E是AB邊上一點,AE=BC,DE⊥EC,取DC的中點F,連接AF、BF. ABCD外作等邊三角形ADF,點E是直角梯形ABCD內一點,且∠EAD=∠EDA=15°,連接EB、EF.
ABCD外作等邊三角形ADF,點E是直角梯形ABCD內一點,且∠EAD=∠EDA=15°,連接EB、EF. 如圖,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2.
如圖,直角梯形ABCD中,AD∥BC,∠BCD=90°,且CD=2AD,tan∠ABC=2. (2013•深圳二模)如圖,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD為邊在直角梯形ABCD外作等邊三角形ADF,點E是直角梯形ABCD內一點,且∠EAD=∠EDA=15°,連接EB、EF.
(2013•深圳二模)如圖,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60°.以AD為邊在直角梯形ABCD外作等邊三角形ADF,點E是直角梯形ABCD內一點,且∠EAD=∠EDA=15°,連接EB、EF.