
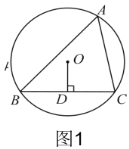
【題目】(1)如圖1,![]() 是
是![]() 的內接三角形,
的內接三角形,![]() 于點
于點![]() .請僅用無刻度的直尺,畫出
.請僅用無刻度的直尺,畫出![]() 中
中![]() 的平分線.(保留作圖痕跡,不寫作法).
的平分線.(保留作圖痕跡,不寫作法).
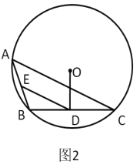
(2)如圖2,![]() 為
為![]() 的外接圓,
的外接圓,![]() 是非直徑的弦,
是非直徑的弦,![]() 是
是![]() 的中點,連接
的中點,連接![]() ,
,![]() 是弦
是弦![]() 上一點,且
上一點,且![]() ,請僅用無刻度的直尺,確定出
,請僅用無刻度的直尺,確定出![]() 的內心
的內心![]() .(保留作圖痕跡,不寫作法)
.(保留作圖痕跡,不寫作法)
【答案】(1)見解析;(2)見解析.
【解析】
(1)延長OD交⊙O于E,依據垂徑定理即可得到E為![]() 的中點,連接AE,則AE平分∠BAC;
的中點,連接AE,則AE平分∠BAC;
(2)依據平行線分線段成比例定理即可得到E為AB的中點,延長OD,OE,根據垂徑定理,即可得到G,F分別為![]() ,
,![]() 的中點,進而得出CF平分∠ACB,AG平分∠BAC,則交點I即為△ABC的內心.
的中點,進而得出CF平分∠ACB,AG平分∠BAC,則交點I即為△ABC的內心.
(1)延長OD交⊙O于E,
∵![]() 于點
于點![]() ,
,
∴E為![]() 的中點,
的中點,
∴AE為∠BAC的平分線,
如圖1所示,AE即為∠BAC的平分線;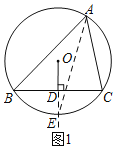
(2)延長OD,OE,交⊙O于G,F,
∵![]() 于點
于點![]() ,
,
∴G為![]() 的中點,
的中點,
∵E為AB的中點,
∴![]() ,
,
∴F為![]() 的中點,
的中點,
∴AG平分∠BAC,CF平分∠ACB,
如圖2所示,點I即為所求.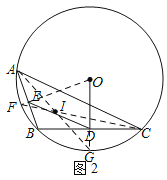


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,點A是拋物線![]() 對稱軸上的一點,連接OA,以A為旋轉中心將AO逆時針旋轉90°得到AO′,當O′恰好落在拋物線上時,點A的坐標為______________.
對稱軸上的一點,連接OA,以A為旋轉中心將AO逆時針旋轉90°得到AO′,當O′恰好落在拋物線上時,點A的坐標為______________.

查看答案和解析>>
科目:初中數學 來源: 題型:
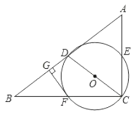
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 為
為![]() 的中點,以
的中點,以![]() 為直徑的
為直徑的![]() 分別交
分別交![]() ,
,![]() 于點
于點![]() ,
,![]() 兩點,過點
兩點,過點![]() 作
作![]() 于點
于點![]() .
.
(1)試判斷![]() 與
與![]() 的位置關系,并說明理由.
的位置關系,并說明理由.
(2)若![]() ,
,![]() ,則
,則![]() 的長為__________.
的長為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=60°,AB=10,BC=4,點P沿線段AB從點A向點B運動,設AP=x.

(1)求AD的長;
(2)點P在運動過程中,是否存在以A、P、D為頂點的三角形與以P、C、B為頂點的三角形相似?若存在,求出x的值;若不存在,請說明理由;
(3)設△ADP與△PCB的外接圓的面積分別為S1、S2,若S=S1+S2,求S的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在銳角△ABC中,∠A、∠B、∠C的對邊分別是a、b、c,其外接圓的半徑為r.
(探究)
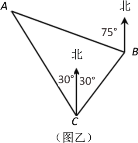
(1)如圖甲,作直徑BD,若r=3,發現![]() 的值為 .
的值為 .
(2)猜想![]() ,
,![]() ,
,![]() 之間的關系,并證明你的猜想.
之間的關系,并證明你的猜想.

(應用)
(3)如圖乙,一貨輪在C處測得燈塔A在貨輪的北偏西30°的方向上,隨后貨輪以60海里/時的速度按北偏東30°的方向航行,半小時后到達B處,此時又測得燈塔A在貨輪的北偏西75°的方向上,求此時貨輪距燈塔A的距離AB.
查看答案和解析>>
科目:初中數學 來源: 題型:
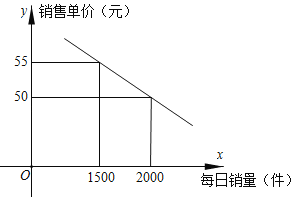
【題目】為倡導節能環保,降低能源消耗,提倡環保型新能源開發,造福社會.某公司研發生產一種新型智能環保節能燈,成本為每件40元.市場調查發現,該智能環保節能燈每件售價y(元)與每天的銷售量為x(件)的關系如圖,為推廣新產品,公司要求每天的銷售量不少于1000件,每件利潤不低于5元.
(1)求每件銷售單價y(元)與每天的銷售量為x(件)的函數關系式并直接寫出自變量x的取值范圍;
(2)設該公司日銷售利潤為P元,求每天的最大銷售利潤是多少元?
(3)在試銷售過程中,受國家政策扶持,毎銷售一件該智能環保節能燈國家給予公司補貼m(m≤40)元.在獲得國家每件m元補貼后,公司的日銷售利潤隨日銷售量的增大而增大,則m的取值范圍是 (直接寫出結果).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC,∠B=90゜,AB=3,BC=6,動點P、Q同時從點B出發,動點P沿BA以1個單位長度/秒的速度向點A移動,動點Q沿BC以2個單位長度/秒的速度向點C移動,運動時間為t秒.連接PQ,將△QBP繞點Q順時針旋轉90°得到△![]() ,設△
,設△![]() 與△ABC重合部分面積是S.
與△ABC重合部分面積是S.
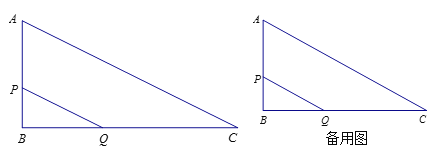
(1)求證:PQ∥AC;
(2)求S與t的函數關系式,并直接寫出自變量t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() .
.
(1)求該函數的圖象與x軸的交點坐標.
(2)已知A(-9,![]() ),B(1,
),B(1,![]() ),C(
),C(![]() ,
,![]() )都在該函數的圖象上,則
)都在該函數的圖象上,則![]() ,
,![]() ,
,![]() 的大小關系為:.
的大小關系為:.
(3)把該函數的圖象沿y軸向什么方向平移多少個單位長度后,與x軸只有一個公共點.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=-2,與x軸的一個交點在(-3,0)和(-4,0)之間,其部分圖象如圖所示.則下列結論:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t為實數);⑤點![]() ,
,![]() ,
,![]() 是該拋物線上的點,則y1<y2<y3.其中正確結論的個數是( )
是該拋物線上的點,則y1<y2<y3.其中正確結論的個數是( )
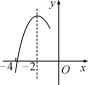
A.4B.3C.2D.1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com